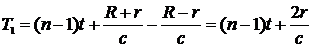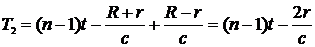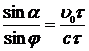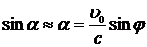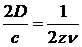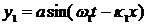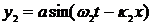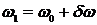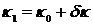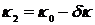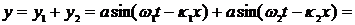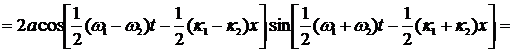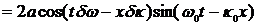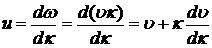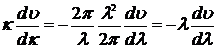Классические опыты по измерению скорости света

Скорость света в свободном пространстве (вакууме) – скорость распространения любых электромагнитных волн, в том числе и световых. Представляет собой предельную скорость распространения любых физических воздействий и инвариантна при переходе от одной системы отсчета к другой.

Задача определения скорости света принадлежит к числу важнейших проблем оптики и физики вообще. Решение этой задачи имело огромное принципиальное и практическое значение. Установление того, что скорость распространения света конечна, и измерение этой скорости сделали более конкретными и ясными трудности, стоящие перед различными оптическими теориями. Первые методы определения скорости света, опиравшиеся на астрономические наблюдения, способствовали со своей стороны ясному пониманию чисто астрономических вопросов. Точные лабораторные методы определения скорости света, выработанные в последствии, используются при геодезической съёмке.

Скорость света в среде зависит от показателя преломления среды n, различного для разных частот n излучения: с’(n) = c/n(n).

Основная трудность, на которую наталкивается экспериментатор при определении скорости распространения света, связана с огромным значением этой величины, требующим совсем иных масштабов опыта, чем те, которые имеют место в классических физических измерениях. Эта трудность дала себя знать в первых научных попытках определения скорости света, предпринятых ещё Галилеем (1607 г.). Опыт Галилея состоял в следующем: два наблюдателя на большом расстоянии друг от друга снабжены закрывающимися фонарями. Наблюдатель А открывает фонарь; через известный промежуток времени свет дойдет до наблюдателя В, который в тот же момент открывает свой фонарь; спустя определенное время этот сигнал дойдет до А, и последний может, таким образом, отметить время τ, протекшее от момента подачи им сигнала до момента его возвращения. Предполагая, что наблюдатели реагируют на сигнал мгновенно и что свет обладает одной и той же скоростью в направлении АВ и ВА, получим, что путь АВ+ВА=2D свет проходит за время τ, т.е. скорость света с=2D/τ. Второе из сделанных допущений может считаться весьма правдоподобным. Современная теория относительности возводит даже это допущение в принцип. Но предположение о возможности мгновенно реагировать на сигнал не соответствует действительности, и поэтому при огромной скорости света попытка Галилея не привела ни к каким результатам; по существу, измерялось не время распространения светового сигнала, а время, потраченное наблюдателем на реакцию. Положение можно улучшить, если наблюдателя В заменить зеркалом, отражающим свет, освободившись таким образом от ошибки, вносимой одним из наблюдателей. Эта схема измерений осталась, по существу, почти во всех современных лабораторных приемах определения скорости света; однако впоследствии были найдены превосходные приемы регистрации сигналов и измерения промежутков времени, что и позволило определить скорость света с достаточной точностью даже на сравнительно небольших расстояниях.

Астрономические методы определения скорости света

Метод Рёмера

Впервые скорость света определил в 1676 году О. К. Рёмер по изменению промежутков времени между затмениями спутников Юпитера.

Юпитер имеет несколько спутников, которые либо видны с Земли вблизи Юпитера, либо скрываются в его тени. Астрономические наблюдения над спутниками Юпитера показывают, что средний промежуток времени между двумя последовательными затмениями какого-нибудь определённого спутника Юпитера зависит от того, на каком расстоянии друг от друга находятся Земля и Юпитер во время наблюдений.

Метод Рёмера (1676 г.), основанный на этих наблюдениях, можно пояснить с помощью рис.9.1. Пусть в определённый момент времени Земля З₁ и Юпитер Ю₁ находятся в противостоянии и в этот момент времени один из спутников Юпитера, наблюдаемый с Земли, исчезает в тени Юпитера. Тогда, если обозначить через R и r радиусы орбит Юпитера и Земли и через с - скорость света в системе координат, связанной с Солнцем, на Земле уход спутника в тень Юпитера будет зарегистрирован на 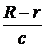 секунд позже, чем он совершается во временной системе отсчёта, связанной с Юпитером.

По истечении 0,545 года Земля З₂ и Юпитер Ю₂ находятся в соединении. Если в это время происходит n-е затмение того же спутника Юпитера, то на Земле оно будет зарегистрировано с опозданием на 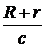 секунд. Поэтому, если период обращения спутника вокруг Юпитера t, то промежуток времени T₁, протекший между первым и n-м затмениями, наблюдавшимися с Земли, равен

.

По истечении ещё 0,545 года Земля З₃ и Юпитер Ю₃ будут вновь находиться в противостоянии. За это время совершились (n-1) оборотов спутника вокруг Юпитера и (n-1) затмений, из которых первое имело место, когда Земля и Юпитер занимали положения З₂ и Ю₂, а последнее - когда они занимали положение З₃ и Ю₃. Первое затмение наблюдалось на Земле с запозданием 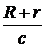, а последнее с запозданием  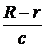по отношению к моментам ухода спутника в тень планеты Юпитера. Следовательно, в этом случае имеем:

.

Рёмер измерил промежутки времени Т₁ и Т₂ и нашёл, что Т₁-Т₂=1980 с. Но из написанных выше формул следует, что Т₁-Т₂=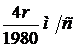, поэтому 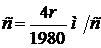. Принимая r, среднее расстояние от Земли до Солнца, равным 150·10⁶ км, находим для скорости света значение: с=301·10⁶ м/с.

Этот результат был исторически первым измерением скорости света.

Определение скорости света по наблюдению аберрации

В 1725-1728 гг. Брадлей предпринял наблюдения с целью выяснить, существует ли годичный параллакс звёзд, т. е. кажущееся смещение звёзд на небесном своде, отображающее движение Земли по орбите и связанное с конечностью расстояния от Земли до звезды. Звезда в своём параллактическом движении должна описывать эллипс, угловые размеры которого тем больше, чем меньше расстояние до звезды.

Для звёзд, лежащих в плоскости эклиптики, этот эллипс вырождается в прямую, а для звёзд у полюса - в окружность. Брадлей действительно обнаружил подобное смещение. Но большая ось эллипса оказалась для всех звёзд имеющие одни и те же угловые размеры, а именно 2α=40",9. Брадлей объяснил (1728 г.) наблюдённое явление, названное им аберрацией света, конечностью скорости распространения света и использовал его для определения этой скорости. Годичный параллакс был установлен более ста лет спустя В. Я. Струве и Бесселем (1837, 1838 гг.).

Для простоты будем вместо телескопа пользоваться визирным приспособлением, состоящим из двух небольших отверстий, расположенных по оси трубы. Когда скорость Земли совпадает по направлению с SE, ось трубы указывает на звезду. Когда же скорость Земли (и трубы) составляет угол j с направлением на звезду, то для того, чтобы луч света оставался на оси трубы, трубу надо повернуть на угол a (рис. 9.2), ибо за время t, пока свет проходит путь SE, сама труба перемещается на расстояние E'Е=u₀t. Из рис. 9.2 можно определить поворот a. Здесь SE определяет направление оси трубы без учёта аберрации, SE' - смещенное направление оси, обеспечивающее прохождение света вдоль оси трубы в течение всего времени t. Пользуясь тем, что угол a очень мал, так как u₀<<с (пренебрегая членами порядка 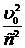), можно считать, что

ÐSE'Р » ÐSEP = j.

Тогда из треугольника E'SE получаем

или .

Если звезда лежит в плоскости эклиптики, то направление вектора скорости Земли u₀ меняется по отношению к направлению на звезду (ES) в течение года по закону 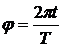, где Т - период обращения Земли, и зависимость угла аберрации от времени выражается периодической функцией .

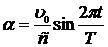К определению скорости света по методу Рёмера

Таким образом, направление на звезду меняется периодически в течение года: звезда совершает кажущееся колебания с угловой амплитудой 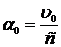 около среднего положения, соответствующего значению j=0 или p.

Если звезда находится в полюсе эклиптики, то j=90° в течение всего года, т. е. угловое отклонение звезды сохраняется неизменным по величине (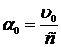); но так как направление вектора u₀ изменяется в течение года на угол 2p, то и угловое смещение звезды меняется по направлению: звезда описывает кажущуюся круговую орбиту с угловым радиусом .

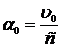В общем случае, когда звезда расположена на угловом расстоянии d от плоскости эклиптики, аберрационная траектория звезды представляет собой эллипс, большая полуось которого имеет угловые размеры a₀, а малая - a₀sind. Именно такой характер и носило кажущееся смещение звёзд по наблюдению Брадлея. Определив из наблюдений a₀ и зная u₀, можно найти с. Брадлей нашёл с=308 000 км/с. В. Я. Струве (1845 г.) значительно улучшил точность наблюдений и получил a₀=20",445. Самые последние определения дают a₀=20",470, чему соответствует с=299 900 км/с.

Следует отметить, что аберрация света связана с изменением направления скорости Земли в течение года.

Лабораторные методы определения скорости света

Лабораторные методы определения скорости света представляют собой, по существу, усовершенствования метода Галилея.

Метод прерываний

Физо (1849 г.) выполнил впервые определение скорости света в лабораторных условиях. Характерной особенностью его метода является автоматическая регистрация моментов пуска и возвращения сигнала, осуществляемая путём регулярного прерывания светового потока (зубчатое колесо). Схема опыта Физо изображена на рис. 9.3. Свет от источника S идёт между зубьями вращающегося колеса W к зеркалу М и, отразившись обратно, должен вновь пройти между зубьями к наблюдателю. Для удобства окуляр Е, служащий для наблюдения, помещается против а, а свет поворачивается от S к W при помощи полупрозрачного зеркала N. Если колесо вращается, и притом с такой угловой скорость, что за время движения света от а к М и обратно на месте зубьев окажутся прорези, и наоборот, то вернувшийся свет не будет пропущен к окуляру и наблюдатель не увидит света (первое затмение). При возрастании угловой скорости свет частично дойдёт до наблюдателя. Если ширина зубьев и просветов одинакова, то при двойной скорости будет максимум света, при тройной - второе затмение и т. д. Зная расстояние аМ=D, число зубьев z, угловую скорость вращения (число оборотов в секунду) n, можно вычислить скорость света.

, или с=2Dzn.

Главная трудность определения лежит в точном установлении момента затмения. Точность повышается при увеличении расстояния D и при скоростях прерываний, позволяющих наблюдать затмения высших порядков. Так, Перротен вёл свои наблюдения при D=46 км и наблюдал затмение 32-го порядка. При этих условиях требуются светосильные установки, чистый воздух (наблюдения в горах), хорошая оптика, сильный источник света.

В последнее время вместо вращающегося колеса с успехом применяют другие, более совершенные методы прерывания света.

Метод вращающегося зеркала

Фуко (1862 г.) успешно осуществил второй метод, принцип которого ещё раньше (1838 г.) был предложен Араго с целью сравнения скорости света в воздухе со скоростью света в других средах (вода). Метод основан на очень тщательных измерениях малых промежутков времени при помощи вращающегося зеркала. Схема опыта ясна из рис. 9.4. Свет от источника S направляется при помощи объектива L на вращающееся зеркало R, отражается от него в направлении второго зеркала С и идёт обратно, проходя путь 2CR=2D за время t. Время это оценивается по углу поворота зеркала R, скорость вращения которого точно известна; угол же поворота определяется из измерения смещения зайчика, даваемого возвратившимся светом. Измерения производятся при помощи окуляра Е и полупрозрачной пластинки М, играющей ту же роль, что и в предыдущем методе; S₁ - положение зайчика при неподвижном зеркале R, S'₁ - при вращении зеркала. Важной особенность установки Фуко явилось применение в качестве зеркала С вогнутого сферического зеркала, с центром кривизны, лежащим на оси вращения R. Благодаря этому свет, отражённый от R к С, всегда попадал обратно на R; в случае же применения плоского зеркала С это происходило бы лишь при определённой взаимной ориентации R и С, когда ось отражённого конуса лучей располагается нормально к С.

Схема опыта метода прерываний

Фуко в соответствии с первоначальным замыслом Араго осуществил при помощи своего прибора также и определение скорости света в воде, ибо ему удалось уменьшить расстояние RС до 4 м, сообщив зеркалу 800 оборотов в секунду. Измерения Фуко показали, что скорость света в воде меньше, чем в воздухе, в соответствии с представлениями волновой теории света.

Последняя (1926 г.) установка Майкельсона была выполнена между двумя горными вершинами, так что в результате получено расстояние D » 35,4 км (точнее, 35 373,21 м). Зеркалом служила восьмигранная стальная призма, вращающаяся со скоростью 528 об/с.

Время, за которое свет совершал полный путь, равнялось 0,00023 с, так что зеркало успевало повернуться на 1/8 оборота и свет падал на грань призмы. Таким образом, смещение зайчика было сравнительно незначительным, и определение его положения играло роль поправки, а не основной измеряемой величины, как в первых опытах Фуко, где всё смещение достигало лишь 0,7 мм.

Были произведены также весьма точные измерения скорости распространения радиоволн. При этом были использованы радиогеодезические измерения, т.е. определение расстояния, между двумя пунктами с помощью радиосигналов параллельно с точными триангуляционными измерениями. Лучшая полученная таким методом величина, приведённая к вакууму, с=299 792±2,4 км/с. Наконец, скорость радиоволн была определена по методу стоячих волн, образованных в цилиндрическом резонаторе. Теория позволяет связать данные о размерах резонатора и резонансной частоте его со скоростью волн. Опыты делались с эвакуированным резонатором, так что приведения к вакууму не требовалось. Лучшее значение, полученное по этому методу, с=299 792,5 ± 3,4 км/с.

Фазовая и групповая скорости света

Лабораторные методы определения скорости света, позволяющие производить эти измерения на коротком базисе, дают возможность определять скорость света в различных средах и, следовательно, проверять соотношения теории преломления света. Как уже неоднократно упоминалось, показатель преломления света в теории Ньютона равен n=sini/sinr=υ₂/υ₁, а в волновой теории n=sini/sinr=υ₁/υ₂, где υ₁ - скорость света в первой среде, а υ₂ - скорость света во второй среде. Ещё Араго видел в этом различии возможность experimentum crucis и предложил идею опыта, который был выполнен позднее Фуко, нашедшим для отношения скоростей света в воздухе и воде значение, близкое к 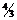, как следует по теории Гюйгенса, а не 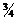, как вытекает из теории Ньютона.

Обычное определение показателя преломления n=sini/sinr=υ₁/υ₂ из изменения направления волновой нормали на границе двух сред даёт отношение фазовых скоростей волны в этих двух средах. Однако понятие фазовой скорости применимо только к строго монохроматическим волнам, которые реально не осуществимы, так как они должны были бы существовать неограниченно долго во времени и выть бесконечно протяжёнными в пространстве.

В действительности мы всегда имеем более или менее сложный импульс, ограниченный во времени и пространстве. При наблюдении такого импульса мы можем выделять какое-нибудь определённое его место, например, место максимальной протяжённости того электрического или магнитного поля, которое представляет собой электромагнитный импульс. Скорость импульса можно отождествить со скоростью распространения какой-либо точки, например, точки максимальной напряжённости поля.

Однако среда (за исключением вакуума) обычно характеризуется дисперсией, т. е. монохроматические волны распространяются с различными фазовыми скоростями, зависящими от их длины, и импульс начинает деформироваться. В таком случае вопрос о скорости импульса становится более сложным. Если дисперсия не очень велика, то деформация импульса происходит медленно и мы можем следить за перемещением определённой амплитуды поля в волновом импульсе, например, максимальной амплитуды поля. Однако скорость перемещения импульса, названная Рэлеем групповой скоростью, будет отличаться от фазовой скорости любой из составляющих его монохроматических волн.

Для простоты вычислений мы будем представлять себе импульс как совокупность двух близких по частоте синусоид одинаковой амплитуды, а не как совокупность бесконечного числа близких синусоид. При этом упрощении основные черты явления сохраняются. Итак, наш импульс, или, как принято говорить, группа волн, составлен из двух волн.

или ,

где амплитуды приняты равными, а частоты и длины волн мало отличаются друг от друга, т.е.

, , , ,

где 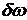и 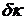- малые величины. Импульс (группа волн) у есть сумма у₁ и у₂, т.е.

.

Вводя обозначения 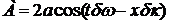, представим наш импульс в виде 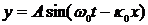, где А не постоянно, но меняется во времени и пространстве, однако меняется медленно, ибо δω и δk - малые (по сравнению с ω₀ и κ₀) величины. Поэтому, допуская известную небрежность речи, мы можем считать наш импульс синусоидой с медленно изменяющейся амплитудой.

Таким образом, скорость импульса (группы), которую, согласно Рэлею, называют групповой скоростью, есть скорость перемещения амплитуды, а, следовательно, и энергии, переносимой движущимся импульсом.

Итак, монохроматическая волна характеризуется фазовой скоростью υ=ω/κ, означающей скорость перемещения фазы, а импульс характеризуется групповой скорость u=dω/dκ, соответствующей скорости распространения энергии поля этого импульса.

Нетрудно найти связь между u и υ. В самом деле,

,

или, так как 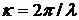 и, следовательно, ,

,

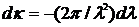т.е. окончательно

(формула Рэлея).

Различие между u и υ тем значительнее, чем больше дисперсия dυ/dλ. В отсутствие дисперсии (dυ/dλ=0) имеем u=υ. Этот случай, как уже сказано, имеет место лишь для вакуума.

Рэлей показал, что в известных методах определения скорости света мы, по самой сущности методики, имеем дело не с непрерывно длящейся волной, а разбиваем её на малые отрезки. Зубчатое колесо и другие прерыватели в методе прерываний дают ослабляющееся и нарастающее световое возбуждение, т.е. группу волн. Аналогично происходит дело и в методе Рёмера, где свет прерывается периодическими затемнениями. В методе вращающегося зеркала свет также перестаёт достигать наблюдателя при достаточном повороте зеркала. Во всех этих случаях мы в диспергирующей среде измеряем групповую скорость, а не фазовую.

Рэлей полагал, что в методе аберрации света мы измеряем непосредственную фазовую скорость, ибо там свет не прерывается искусственно. Однако Эренфест (1910 г.) показал, что наблюдение аберрации света в принципе  неотличимо от метода Физо, т.е. тоже даёт групповую скорость. Действительно, аберрационный опыт можно свести к следующему. На общей оси жёстко закреплены два диска с отверстиями. Свет посылается по линии, соединяющей эти отверстия, и достигает наблюдателя. Приведём весь аппарат в быстрое вращение. Так как скорость света конечна, то свет не будет проходить через второе отверстие. Чтобы пропустить свет, необходимо повернуть один диск относительно другого на угол, определяемый отношением скоростей дисков и света. Это - типичный аберрационный опыт; однако он ничем не отличается от опыта Физо, в котором вместо двух вращающихся дисков с отверстиями фигурирует один диск и зеркало для поворота лучей, т.е. по существу два диска: реальный и его отражение в неподвижном зеркале. Итак, метод аберрации даёт то же, что и метод прерываний, т.е. групповую скорость.

Таким образом, в опытах Майкельсона и с водой, и с сероуглеродом измерялось отношение групповых, а не фазовых скоростей.