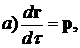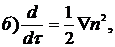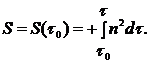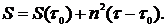Понятие луча

Решение задачи по определению поля в неоднородной среде следует начинать с нахождения эйконала S. Зная эту функцию, можно построить волновые фронты: они задаются уравнением S=const, а затем и лучи - линии, перпендикулярные волновому фронту.

Следует заметить, что вообще эйконал в большей степени определяет световое поле, чем амплитуда А₀(r). Это объясняется тем, что перед S(k,r) стоит большой множитель k. Поэтому все изменения u при малом изменении координат определяются главным образом изменением S, а не А₀.

Уравнение (6) решается в наиболее общем виде с помощью метода характеристик. Этот метод сводит уравнение в частных производных к системе обыкновенных дифференциальных уравнений. Обозначим 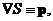 введем параметр τ вдоль направления p, связанный с длиной дуги l на луче условием dl/dτ=n. Вектор r определяет точку на луче, а вектор dr/d 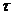является касательным к лучу. Уравнение (6) выглядит в новых обозначениях как |p|=n. Можно показать, что оно эквивалентно следующей системе уравнений:

(1)

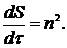(2)

Уравнения (1) определяют геометрию лучей

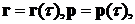(3)

т.е. координаты r и направления p луча в точке с параметром τ (этот параметр пропорционален времени прохождения волны вдоль луча). Очевидно, что касательный к лучу вектор (1) параллелен 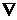 S, т.е. перпендикулярен к волновой поверхности. Таким образом, луч есть нормаль к поверхности равной фазы.

Вектор p, определяющий направление луча, изменяется вдоль луча, согласно (2), в направлении градиента показателя преломления. Иными словами, преломление, или рефракция, криволинейного луча в неоднородной среде происходит в область возрастания n.

В частном случае однородной среды 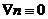, так что p=const, и лучи являются прямыми линиями.

Для эйконала из (2) получаем

(4)

Здесь 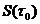 - значение эйконала при 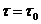; интегрирование ведется вдоль геометрооптического луча. Заметим, что в геометрической оптике физическое значение имеет лишь разность эйконалов 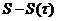, а не величина S.

Для однородной среды

Выбрав направление оси z вдоль луча, умножив затем эйконал - его часто называют "оптический путь" - на частоту k, получим привычное выражение для фазы плоской волны kn(z-z₀), так как, очевидно, в данном случае nτ =z.

Рис. 3.1. Система лучевых координат

Для построения лучей и фронтов удобно пользоваться системой лучевых координат (рис. 3.1).

Такими координатами являются две координаты ξ, η на поверхности любого, принятого за начальный, волнового фронта 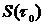, характеризующие данный луч и постоянные вдоль луча, и длина дуги l , отсчитываемая вдоль луча, либо вместо r - введенный выше параметр 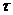(время).