Понятие об общей теории центрированных оптических систем

Гаусс (1841 г.) дал общую теорию оптических систем, получившую дальнейшее развитие в трудах многих математиков и физиков. Теория Гаусса есть теория идеальной оптической, системы, т.е. системы, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету. Согласно этому определению всякой точке пространства объектов соответствует в идеальной системе точка пространства изображений; эти точки носят название сопряженных. Точно так же каждой прямой или плоскости пространства объектов должна соответствовать сопряженная прямая или плоскость пространства изображений. Таким образом, теория идеальной оптической системы есть чисто геометрическая теория, устанавливающая соотношение между точками, линиями, плоскостями.

Идеальная оптическая система может быть осуществлена с достаточным приближением в виде центрированной оптической системы, если ограничиться областью вблизи оси симметрии, т.е. параксиальными пучками. В теории Гаусса требование «тонкости» системы отпадает, но лучи по-прежнему предполагаются параксиальными. Разыскание оптической системы, которая приближалась бы к идеальной даже при пучках значительного раскрытия, есть такая задача прикладной геометрической оптики.

Случай преломления на одной сферической поверхности сравни­тельно редок. Большинство реальных преломляющих систем со­держит по крайней мере две преломляющие поверхности (линза) или большее их число.

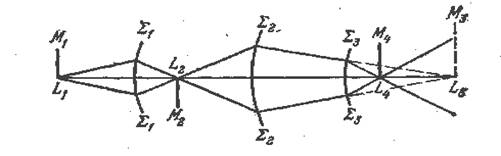
Рис. 3.13. Центрированная оптическая система

Система сферических поверхностей называется центрированной, если центры всех поверхностей лежат на одной прямой (рис. 3.13.).

Линия, соединяющая центры сферических поверхностей, представляет собой ось симметрии центрированной системы и называется главной оптической осью системы. Теория Гаусса устанавливает ряд так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы и позволяет пользоваться ею, не рассматривая реального хода лучей в системе.

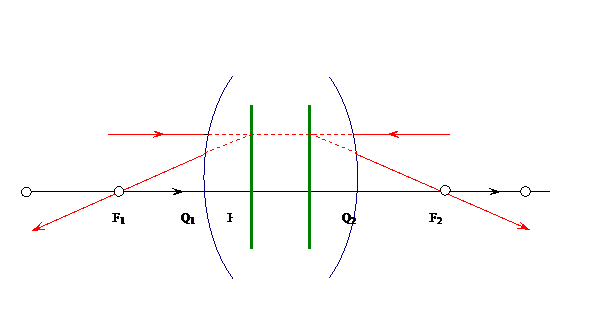
Рис. 3.14. Главные оптические плоскости H1R1 и H2R2 и фокусы F1 и F2 оптической системы

Пусть ММ и NN - крайние сферические поверхности, ограничивающие систему, и ОО₁ - ее главная ось (рис. 3.14.). Проведем луч А₁В₁, параллельный О₁О₂; точка В₁ есть место входа этого луча в систему. Согласно свойству идеальной системы лучу А₁В₁ соответствует в пространстве изображений сопряженный луч G₂F₂, выходящий из системы в точке G₂ . Как идет луч внутри системы нас не интересует. Второй луч  P₁Q₁ выберем вдоль главной оси. Сопряженный ему луч Q₂P₂ будет также идти вдоль главной оси. Точка F₂ как пересечение двух лучей G₂F₂ и Q₂P₂ есть изображение точки, в которой пересекаются лучи А₁В₁ и P₁Q₁, сопряженные с G₂F₂ и Q₂P₂ . Но так как А₁В₁││P₁Q₁, то точка, сопряженная с F₂, лежит в бесконечности. Таким образом, F₂ есть фокус (второй, или задний) системы. Плоскость, проходящая через фокус перпендикулярно к оси, носит название фокальной.

Любая точка линии H₁R₁ сопряжена с точкой линии H₂R₂, лежащей на такой же высоте от О₁О₂ , как и выбранная. То же относится и к плоскостям, проведенным через H₁R₁ и H₂R₂ перпендикулярно к главной оси, т.к. вся система симметрична относительно оси.

Итак, плоскость H₁R₁, изображается на H₂R₂ прямо и в натуральную величину. Такие плоскости называются главными плоскостями. Таким образом, идеальная оптическая система обладает главными плоскостями. Точки H₁ и H₂ пересечения главных плоскостей с осью носят название главных точек системы. Расстояния от главных точек до фокусов называются фокусными расстояниями системы f₁ = H₁R₁ и f₂ = H₂R₂.