Эффект Керра

А. Общие сведения. Возникновение анизотропии под действием внешнего электрического поля представляет собой явление, с теоретической стороны значительно глубже разработанное, чем явления, изученные в предыдущем параграфе и имеющее поэтому гораздо большее значение как для понимания механизма анизотропии вообще, так и для вопросов, связанных с исследованием молекулярной структуры. Причина этого лежит прежде всего в том, что явление Керра удалось наблюдать в гораздо более простых для теоретической трактовки условиях, а именно в газах, хотя первые наблюдения относились к твердым телам и жидкостям, в которых этот эффект выражен значительно сильнее. Кроме того, механизм воздействия внешнего однородного электрического поля на молекулы гораздо проще и понятнее, чем эффекты механических деформаций, трактовка которых требует исследования воздействия на молекулы междумолекулярных электромагнитных полей, изменяющихся вследствие деформаций, т.е. исследования влияния очень сложного и плохо изученного фактора.

Вместе с тем явление Керра нашло за последние годы ряд чрезвычайно важных научных и научно-технических применений, основанных на способности его протекать практически безынерционно, т.е. следовать за очень быстрыми переменами внешнего поля. Таким образом, и по теоретической, и по практической ценности явление двойного лучепреломления в электрическом поле принадлежит к числу крайне интересных и важных. Как уже упоминалось, о желательности постановки подобных опытов писал еще Ломоносов (1756 г.); о неудаче попытки обнаружить, влияет ли электризация на преломляющую способность жидкости, сообщает Юнг (1800 г.); и лишь в 1875 г. были выполнены опыты Керра, надежно установившие явление. Керр показал, что многие жидкие диэлектрики становятся анизотропными под действием электрического поля. Опыты с жидкими диэлектриками имеют решающее значение, ибо для жидких веществ деформация, могущая возникнуть под действием электрического поля (электрострикция), не вызывает двойного лучепреломления, так что в опытах с жидкостью мы имеем электрооптические явления в чистом виде. Описанный Керром эффект стал первым доказательством того, что оптические свойства вещества могут изменяться под влиянием электрического поля.

Наряду со знаменитым явлением Фарадея (вращение плоскости поляризации в магнитном поле, 1846 г.), которое было первым исследованным магнитооптическим эффектом, явление Керра сыграло важную роль в обосновании электромагнитной теории света. В более поздние годы (1930 г. и позже) удалось наблюдать двойное лучепреломление под действием электрического поля в парах и газах. Измерения эти гораздо труднее измерений в жидкостях вследствие малости эффекта, зато теория явления приложима к ним с меньшими оговорками.

Б. Методы наблюдения и экспериментальные данные. Под влиянием электрического поля вещество становится в оптическом отношении подобным одноосному кристаллу с оптической осью вдоль направления электрической напряженности, являющегося осью симметрии (рис. 6.8). Главные плоскости поляризаторов N₁ и N₂ составляют с направлением поля угол, отличный от нуля (лучше всего 45°).

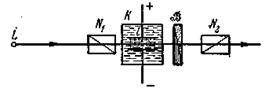
Рис. 6.8 Схема расположения приборов для наблюдения двойного лучепреломления в электрическом поле

Если поляризаторы скрещены и электрическое поле не наложено, то свет не проходит через нашу систему. При наложении электрического поля жидкость между обкладками конден-сатора становится двоякопреломляющей, так что свет, выходящий из K, оказывается эллиптически-поляризован-ным и может быть исследован при помощи конденсатора В.

Опыт показывает, что для монохроматического света данной длины волны λ разность показателей преломления n_о и n_е пропорциональна квадрату напряженности поля E:

n_о-n_е=kЕ² (11)

и следовательно разность хода, приобретаемая лучами на пути l равна

δ=l(n_о-n_е)=klЕ² (12)

(здесь и дальше предполагается, что поле однородно, а луч перпендикулярен к направлению поля).

Выражая эту разность в длинах волн, получаем сдвиг фазы

j=2πδ/λ=2πlBE² (13)

где В=к/λ - постоянная Керра.

Как видно из квадратичной зависимости δ от Е, сдвиг фазы не зависит от направления поля.

Для большинства жидкостей n_о>n_е, т.е. В>0: их анизотропия соответствует анизотропии положительного кристалла. Есть, однако, жидкости, для которых В<0 (например, этиловый эфир, многие масла и спирты). Численные значения постоянной Керра для разных веществ весьма различны. Максимальным значением В среди всех известных веществ обладает нитробензол, для которого приблизительно В=2×10^-5 СГСЭ. Таким образом, если, например, на обкладки конденсатора длиной l=5 см с расстоянием между ними d=1 мм наложена разность потенциалов в 1500 В, т.е. напряженность поля равна 15 000 В/см=50 СГСЭ, то разность фаз в нитробензоле достигает π/2, иными словами, такой конденсатор Керра действует, как пластинка в четверть волны. Понятно, что нетрудно обнаружить гораздо меньшую разность фаз, и, следовательно, опыты с нитробензолом не наталкиваются на какие-либо трудности, связанные с чувствительностью. Поэтому нитробензол находит себе широкое применение во всех технических устройствах.

Для других жидкостей постоянная Керра значительно меньше; например, для хлорбензола она равна 10×10^-7, для воды 5×10^-7, для сероуглерода 3,5×10^-7, для бензола 0,5×10^-7 СГСЭ. Еще меньше постоянная Керра для газов. Так, для парообразного сероуглерода (при давлении 900 мм рт. ст. и температуре 57 °С) В=3,6×l0^-10, для парообразного нитробензола 27×10^-10, а для такого газа, как азот, всего лишь 0,4×10^-10 СГСЭ.

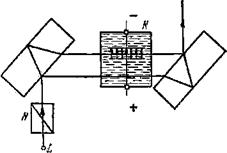
Рис. 6.9. Схема интерференционного метода наблюдения разности (nе-n) или (nо-n) при двойном лучепреломлении.

Из приведенных данных, относящихся к длине волны l=546,0 нм (зеленая линия), видно, насколько трудно исследование явления Керра в газах. В первых измерениях этого рода применялся конденсатор с длиной пластин 50 см и с расстоянием между ними около 4 мм, на которые накладывалась разность потенциалов 15 000 - 20 000 В, так что напряженность поля достигала 40000 - 50000 В/см и получающаяся разность хода измерялась с помощью специальных анализаторов с точностью до 5×10^-6 длины волны.

Постоянная Керра увели­чивается при уменьшении длины волны (дисперсия) и сильно уменьшается при по­вышении температуры.

В обычной схеме наблюдения определяется только разность n_о-n_е; можно, однако, определить и значения n_о и n_е в отдельности. Для этой цели измеряют разность n_е-n или n_о-n, т.е. разность между показателем преломления необыкновенного (или обыкновенного) луча и показателем преломления вещества вне электрического поля.

Такие определения можно выполнить интерференционным методом по схеме рис. 6.9. Сущность этого метода, принадлежащего Л. И. Мандельштаму, состоит в том, что один из лучей в интерферометре Жамена пропускают через жидкость, помещаемую в электрическое поле (между пластинками конденсатора, расположенного в кювете К), а другой луч направляют через жидкость, находящуюся вне электрического поля. Измеряя смещение полос интерференционной картины при включении электрического поля, определяем n_е-n или n_о-n в зависимости от первоначальной установки поляризатора N. Если поляризатор установлен так, что колебания вектора электрического поля света происходят параллельно внешнему полю (вдоль «оптической оси»), то наблюдаемое смещение полос определяет величину    n_е-n; при повороте поляризатора на 90° - величину n_о-n.

Результаты тщательных измерений величин n_е-n и n_о-n дают (для большинства веществ)

(14)

В). Явление Керра, вызванное электрическим полем мощного импульса света. Выше речь шла о возникновении двойного лучепреломления в изотропной среде под действием постоянного электрического поля. Такое же явление наблюдается и в переменном электрическом и даже в поле световой волны.

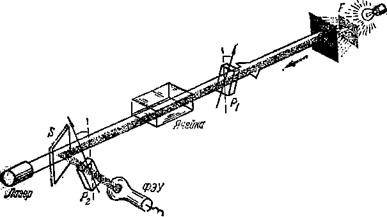
Рис. 6.10. Принципиальная схема опыта по созданию двойного лучепреломления под действием мощного импульса света.

Развитие лазерной техники позволило генерировать импульсы света с напряженностью электрического поля, достигающей очень больших значений, и экспериментально доказа-но, что под действием поля мощного импульса света в жидкостях возникает двойное лучепреломление. В первом опыте такого рода (Майер и Жирэ, 1964 г.) длительность импульса света составляла 5,5×10^-8 с, энергия 0,14 Дж, а среднеквадратичная напряженность 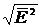=39 кВ/см. Принципиальная схема опыта показана на рис. 6.10. После светофильтра F голубой свет (λ=500 нм) справа налево проходит через ячейку, наполненную изучаемой жидкостью, и, отразившись от пластинки S, попадает на фотоумножитель ФЭУ. При скрещенных поляризаторах (как на рис. 6.10) голубой свет не может попасть в ФЭУ.

Если в такую установку слева направо входит мощный импульс света, то он вызывает в жидкости двойное лучепреломление, и голубой свет будет попадать на ФЭУ, пока импульс проходит через ячейку с жидкостью. Для определения постоянной Керра В измеряется разность хода δ (см. (12)), создаваемая под действием поля лазерного импульса, а затем в ячейке такой же длины и с тем же веществом добиваются той же разности хода, накладывая постоянное поле. Оказалось, что равные разности хода в случае бездипольных молекул жидкости создаются практически равными напряженностями поля, что означает равенство постоянных Керра в статическом поле и при световой частоте.

Однако для дипольных молекул результат оказывается существенно иным. Например, для нитробензола постоянная Керра в поле световой частоты приблизительно в 100 раз меньше, чем в статическом или квазистатическом поле.

Г. Основы теории явления. С молекулярной точки зрения объяснение явления Керра лежит в оптической анизотропии молекул жидкости или газа, в которых наблюдается этот эффект. Такие анизотропные молекулы в поле световой волны обнаруживают большую или меньшую поляризуемость в зависимости от ориентации их по отношению к электрическому вектору световой волны. Однако в обычных условиях молекулы, составляющие среду, расположены вполне хаотически, так что при распространении световой волны с любым направлением электрического вектора и по любому направлению она будет встречать в среднем одинаковые условия: среда ведет себя как макроскопически изотропная. Но если наложение достаточно сильного электрического поля вызовет преимущественную ориентацию молекул, то некоторое направление в среде окажется направлением большей поляризуемости, чем другие. Поэтому и скорость распространения световых волн будет зависеть от расположения электрического вектора волны внутри среды, т. е. от направления распространения световых волн и характера их поляризации: среда приобретает анизотропный характер.

Так как внешнее электрическое поле является осью симметрии, то диэлектрические проницаемости вдоль поля и в перпендикулярном направлении будут различны; но все направления, перпендикулярные к направлению поля, равноправны. Выбрав оси координат вдоль поля (z) и в двух взаимно перпендикулярных направлениях, например вдоль луча (у) и перпендикулярно к нему (х), получим три главных направления со значениями диэлектрической проницаемости ε_z, ε_x=ε_y. Таким образом, эллипсоид диэлектрической проницаемости есть эллипсоид вращения, и среда подобна одноосному кристаллу, причем направление электрического поля представляет собой оптическую ось.

Ориентация анизотропных молекул под действием внешнего электрического поля может происходить двояким образом. Первоначальная, теория (Ланжевен, 1910 г.) рассматривала молекулы, которые не имеют собственного электрического момента, но приобретают его под действием внешнего поля. В первом приближении величину приобретенного молекулой момента μ можно считать пропорциональной напряженности внешнего поля Е, т. е. μ=кЕ. Для анизотропных молекул к зависит от направления внутри молекулы, и μ, не совпадает с направлением действующего поля. Поэтому возникает пара сил, момент которой стремится ориентировать молекулы осью наибольшей поляризуемости вдоль поля. Таким образом, среда становится анизотропной. Направление этого момента остается неизменным при изменении направления поля на противоположное, и поэтому даже при световых частотах поля происходит ориентация молекул.

Если на среду падает свет, то наибольший показатель преломления будут иметь волны, электрический вектор которых направлен вдоль линии максимальной поляризуемости, т.е. вдоль внешнего поля. Так как направление внешнего поля играет по отношению к среде роль оптической оси, то, следовательно, волна с наибольшим показателем преломления есть волна необыкновенная (колебание .вдоль оси), т. е. n_о>n_е и В>0.

Таким образом, теория Ланжевена объясняет явление Керра, но оставляет непонятным существование (хотя и в меньшем количестве) веществ, для которых n_о<n_е, т. е. В<0.

Борн (1916 г.) дополнил теорию Ланжевена, приняв во внимание возможность существования молекул со значительным постоянным электрическим моментом, направление которого может не совпадать с направлением наибольшей поляризуемости. В таком случае молекула ориентируется внешним полем так, что по направлению внешнего поля стремится установиться ее постоянный момент, а направление наибольшей поляризуемости (т.е. наибольшей диэлектрической проницаемости) может составить заметный угол с направлением внешнего поля (играющим роль оптической оси). В зависимости от взаимного расположения этих двух направлений вещество может характеризоваться положительным или отрицательным значением постоянной Керра В. В частности, если направление максимальной поляризуемости совпадает с направлением постоянного момента, то В>0; если они взаимно перпендикулярны, то В<0. При некотором промежуточном положении В может равняться нулю, т.е. вещество не обнаруживает явления Керра. Отсюда понятно, почему вещества с близкими электрическими моментами и не сильно различающимися поляризуемостями (показателями преломления) могут очень сильно отличаться по отношению к эффекту Керра. Так, метилбромид имеет постоянную Керра, в сотни раз большую, чем метиловый спирт, хотя электрические моменты их и поляризуемости отличаются незначительно.

При световых частотах внешнего поля дипольная молекула, вследствие своей инерционности, не успевает ориентироваться в такт с изменениями направления напряженности поля; следовательно, постоянный дипольный момент молекулы перестает вносить свой вклад в постоянную Керра. Поэтому при световых частотах внешнего поля постоянная Керра нитробензола, например, в 100 раз меньше, чем в статическом поле.

Молекулярно-кинетическое вычисление анизотропии, возникающей под действием электрического поля, требует статистического учета всех возможных ориентации молекул под действием внешнего поля Е и теплового движения. Оно приводит к результатам, согласным с опытом, а именно: постоянная Керра должна быть пропорциональна квадрату напряженности внешнего поля и уменьшается с увеличением температуры, ибо под действием тепловых столкновений расстраивается ориентация молекул, определяющая возникновение анизотропии.

Как уже упоминалось, ориентационная теория может претендовать на количественное совпадение с опытом только в случае газов, когда можно не учитывать взаимодействия между молекулами, характерные для жидкостей.

Д. Время существования явления Керра. Некоторые применения ячейки Керра. Измерение времени существования явления Керра было начато Абрагамом и Лемуаном (1899 г.) и несколько раз повторялось вплоть до 1939г. Во всех этих работах не удавалось измерить искомое время с удовлетворительной точностью, но можно было только сказать, что оно меньше 10^-8 с, а в некоторых случаях даже меньше 10^-9 с.

Рис. 6.11. Схема для определения времени исчезновения двойного лучепре­ломления.

Количественное определение времени существования явле-ния Керра удалось произвести только с применением мощ-ных и коротких импульсов лазерного света. На рис. 6.11 представлена схема опыта. Мощный импульс света с длиной волны λ=1,06 мкм и длительностью порядка 10^-12 с проходит через кристалл дигидрофосфата калия KН₃Р0₄(KDP), в котором небольшая его часть превращается в свет с удвоенной частотой, т.е. его длина волны λ =0,53 мкм. Зеркало S₁ пропускает инфракрасный свет и отражает зеленый, а зеркало S₂ пропускает зеленый и отражает инфракрасный. За зеркалом S₂ расположена ячейка с изучаемым веществом между скрещенными поляризаторами P₁ и P₂. После P₂ помещается светофильтр F, отсекающий инфракрасный и пропускающий на фотоумножитель ФЭУ только зеленый свет. Можно так расположить детали установки, чтобы оптические пути зеленого и инфракрасного лучей были одинаковыми, С помощью пластинок стекла D различной толщины можно задерживать прибытие зеленого луча в ячейку на различные промежутки времени. Устройства различной конструкции, позволяющие создавать задержку в прибытии одного сигнала относительно другого, носят название линий задержки. Мощный импульс инфракрасного излучения создает в ячейке двойное лучепреломление, в результате которого зеленый свет также проходит через всю систему и достигает фотоумножителя.

Если зеленый свет дойдет до ячейки раньше мощного импульса или много позже его, то он, разумеется, не сможет достигнуть фотоумножителя.

Во всех промежуточных случаях, которые можно осуществлять, меняя величину задержки, на фотоумножитель будет попадать нарастающее количество света, которое достигнет максимума и затем начнет уменьшаться. Как показывают расчеты, время существования явления Керра, или, что то же самое, время релаксации анизотропии, может быть определено из хода убывания интенсивности света зеленого импульса в зависимости от разности времен прихода обоих импульсов.

Такие измерения показали, что время релаксации анизотропии в сероуглероде равно 2×10^-12 с, а в нитробензоле 50×10^-12 с. Полученные таким способом данные находятся в хорошем согласии с косвенными методами измерения этих величин.

Ячейка Керра, работающая в электрическом поле короткого мощного светового импульса, может служить фотографическим затвором, который позволяет делать время экспозиции порядка 10^-12 с. Она с успехом применяется для изучения длительности люминесценции и других молекулярных процессов. Ячейка Керра, подобная изображенной на рис. 6.11, может служить для модуляции интенсивности света; необходимо только питать конденсатор напряжением высокой частоты.

Если к обкладкам конденсатора. Керра подавать импульс напряжения, то ячейка играет роль затвора, длительность действия которого определяется длительностью электрического импульса.

Ячейки Керра как модулятор и затвор применяются для управления режимом работы оптических квантовых генераторов.

Благодаря чрезвычайной быстроте установления и исчезновения эффекта Керра оказалось возможным использовать его для многих научных и технических целей.