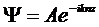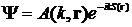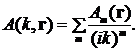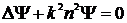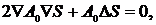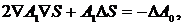Приближение геометрической оптики

Возможны две точки зрения на место геометрической оптики в системе современных оптических представлений. Согласно первой из них, геометрическая оптика рассматривается как самостоятельный раздел оптики, основанный на определенной системе постулатов. К наиболее важным из них относятся законы прямолинейного распространения света, законы его отражения и преломления. В такой постановке геометрическая оптика является основой вычислительной оптики, на базе которой осуществляются расчеты разнообразных оптических элементов и систем. Согласно второй точке зрения, основные выражения и соотношения аппарата геометрической оптики являются по своей сути приближенными решениями волновых уравнений, во многих случаях облегчающих их анализ. Исходя из целевой установки данной книги, мы будем придерживаться второй точки зрения.

При этом сосредоточимся на вопросах распространения света в неоднородной среде, показатель преломления которой плавно меняется в пространстве. Световое поле представляется в форме локально плоской волны. В приближении геометрической оптики амплитуда этой волны не зависит от частоты, а частота, которая считается большой величиной, входит только в фазовый множитель.

В однородной (n=const) среде простейшее решение волнового уравнения - плоская волна

. (1)

Фаза ее постоянна на плоскостях z=cоnst, т.е. фазовые фронты плоские. Нормали к фронтам параллельны.

Пусть показатель преломления среды есть функция координат n=n(r), тогда амплитуда А становится функцией координат, а волновые фронты перестают быть плоскими. Нормали к ним не параллельны, но близки к параллельным. Будем считать, что все характерные масштабы изменения и амплитуды поля, и показателя преломления среды велики по сравнению с длиной волны 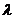 (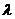=2p/k). Если l - наименьший из этих масштабов, то предполагается, что выполнено неравенство

Это неравенство - не самое сильное условие применимости лучевой или геометрической оптики, законы которой мы ниже сформулируем. Представим поле световой волны в неоднородной среде в виде почти плоской волны

(3)

Здесь А(k,r) - амплитуда волны; kS(r) - фаза; величина S(r) называется эйконалом. Термин "почти плоская волна" оправдан тем, что в области порядка 2p/kn поле имеет вид (1).

Амплитуду А и эйконал S будем искать из требования, чтобы решение, записанное в форме (3), удовлетворяло волновому уравнению, и при этом используем условие, что k велико. Это можно сделать несколькими способами. Простейший из них состоит в том, чтобы искать А в виде лучевого разложения по обратным степеням k:

(4)

Фактически это разложение проводится по возрастающим степеням безразмерного малого параметра μ (2).

Подставляя (3), (4) в волновое уравнение

(5)

и приравнивая нулю коэффициенты при одинаковых степенях k, получим в нулевом приближении уравнение эйконала

(6)

а в следующих приближениях - систему рекуррентных уравнений для амплитуд

(7)

(8)

которые называются уравнениями переноса.

Приближение, при котором в (4) сохраняется только нулевой член, называется геометрооптческим приближением. Поля в этом приближении, т.е. поля геометрической оптики

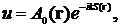
(9) Приближение геометрической оптики

содержат частоту только множителем в фазе. В отличие от (3), в (9) А₀ уже не есть функция частоты.