Дифракция Френеля на круглом отверстии и круглом экране
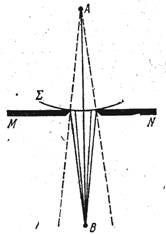
Пусть волна å, идущая из А, встречает на пути экран MN с круглым отверстием. Исследуем явление в точке В, лежащей на линии, соединяющей А с центром круглого отверстия.
Вспомогательная поверхность Френеля å будет касаться экрана MN. Разбивка на зоны Френеля, произведенная, покажет, что в зависимости от размера отверстия в нем уложится большее или меньшее число зон. При небольшом размере отверстия и соответственных расстояниях А и В можно учитывать лишь ограниченное число действующих зон. Легко видеть, что если отверстие открывает всего лишь одну зону или небольшой нечетное число зон, то действие в точке В будет больше, чем при отсутствии экрана. Максимум действия соответствует размеру отверстия в одну зону. Если же отверстие открывает четное число зон, то световое возбуждение в точке В будет меньше, чем при свободной волне. Наименьшая освещенность соответствует двум открытым зонам диаграммы, и определяющие световое возбуждение в точке В зависимости от числа зон, укладывающихся в отверстии.
Дифракция на круглом отверстии
Аналогичная картина будет наблюдаться для любой точки, лежащей на линии АВ. Расчет картины для точек, лежащих в плоскости, перпендикулярной к АВ, в стороне от этой линии, несколько сложнее. Но легко увидеть, что вследствие симметрии всего расположения вокруг линии АВ распределение света в указанной плоскости должно быть симметрично, т.е. области одинаковой освещенности должны располагаться кольцеобразно около точки В. При подходящих условиях опыта можно наблюдать несколько концентрических областей максимумов и минимумов освещенности, плавно переходящих друг в друга. Дифракция на круглом отверстии
Дифракция на круглом отверстии
Дифракция на круглом экране
Для точки В, лежащей на линии, соединяющей источник А с центром экрана, построение Френеля дает первую зону от края экрана до линии пересечения поверхности волны с конусом, образующая которого равна b+½l, вторую зону - до конуса с образующей b+l. Повторяя рассуждение получим, что амплитуда световых колебании в B равна половине амплитуды, обусловленной первой открытой зоной.

Картины дифракции на круглом отверстии

Картины дифракции на круглом отверстии
Картины дифракции на круглом отверстии
Если размер экрана невелик, то действие первой открытой зоны практически не отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке В будет такой же как и в отсутствии экрана. Вследствие симметрии всей картины относительно прямой АВ светлая точка в В окружена кольцевыми зонами чередующихся тени и света. По мере удаления от В в направлении, перпендикулярном линии АВ, кольца становятся все менее и менее резкими, пока вдали от В не получится равномерная освещенность.
Парадоксальное на первый взгляд заключение, в силу которого в самом центре геометрической тени должна находится светлая точка, было выдвинуто Пуассоном в 1818 при рассмотрении мемуара Френеля в Парижской академии, в качестве доказательства несостоятельности рассуждений Френеля. Однако Арго произвел соответствующий опыт и показал, что выводы Пуассона соответствуют действительности и лишь подтверждают теорию Френеля. Светлое пятно в центре геометрической тени, предсказанное Пуассоном в качестве мнимого опровержения волновой природы света, получило наименование пятна Пуассона.
Для успеха опыта необходимо, чтобы край экрана хорошо совмещался с границами зоны. Удобным для этой цели являются стальные шарики от шарикоподшипников. В этом случае, когда края экрана имеют неровности, сравнимые с размерами первой открытой френелевой зоны, расчет и опыт показывает, что экранчик нарушит однозначные предсказания теории Френеля о наличии пятна Пуассона.
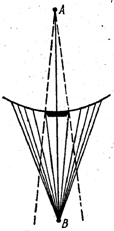
Схема дифракции на круглом диске

Картина дифракции на круглом диске