Практическое занятие 8
Задача 1.
Масса нейтрального атома 16O mат(A,Z) = 15.9949 а.е.м. Определить удельную энергию связи ядра 16O.
Решение.
Удельная энергия связи ядра
(A,Z) = Eсв(A,Z)/A,
где Eсв (A,Z) — энергия связи ядра, A — массовое число. Полная энергия связи ядра
Eсв (A,Z) = [Zmp + (A-Z)mn - mя(A,Z)]c2 = [Zmp + (A-Z)mn - mат(A,Z) - Zme]c2
Используя энергетические единицы для масс 1а.е.м.= 931.49 МэВ, получаем для ядра 16O
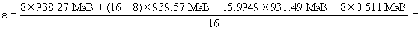
= 7.5 МэВ/нуклон.
Задача 2.
На каком расстоянии интенсивность пучка мюонов с кинетической энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины первоначального значения?
Решение.
Уменьшение интенсивности пучка мюонов происходит в результате распада мюонов
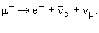
Число мюонов N(t), не распавшихся к моменту времени t, определяется соотношением
N(t) = N(0) exp(-t/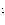
), (1)
где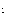 
- среднее время жизни мюона, N(0) — число мюонов в начальный момент времени. Среднее время жизни покоящихся мюонов равно 2.2·10- 6 с. В данном случае
N(t) = N(0)/2 = N(0) exp(-t/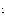
), (2)
то есть exp(- t/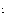
) = 1/2, или же t = 
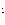ln2. Релятивистское замедление течения времени определяется соотношением
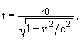(3)
где t0 — время в системе, связанной с движущимся телом. В нашем случае получаем
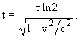(4)
Связь между кинетической энергией T и импульсом p частицы
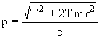(5)
Релятивистский импульс частицы
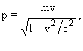(6)
где m — масса покоя частицы, v — ее скорость. Из (5) и (6) получим
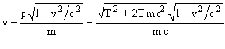(7)
Энергия покоя mc2 мюона 106 МэВ. Пробег мюона
l = vt (8)
Подставляя в (8) (4) и (7), получим
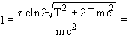
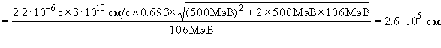
Задача 3.
Массы нейтральных атомов в а.е.м.: 16O — 15.9949, 15O — 15.0030, 15N — 15.0001. Чему равны энергии отделения нейтрона и протона в ядре 16O?
Решение.
Энергия отделения нейтрона
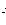n(A,Z) = mn +m(A-1,Z) — m(A,Z),
протона
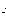p(A,Z) = mp +m(A-1,Z-1) — m(A,Z).
В обеих формулах массы должны быть в энергетических единицах.
Для ядра 16O
n = 939.6 МэВ + (15.0030 а.е.м. — 15.9949 а.е.м.)х931.5 МэВ = 15.6 МэВ,
p = 938.3 МэВ + (15.0001 а.е.м. — 15.9949 а.е.м.)х931.5 МэВ = 15.6 МэВ.
Ядро 10B из возбужденного состояния с энергией 0.72 МэВ распадается путем испускания 
-квантов с периодом полураспада T1/2 = 6.7·10-10 с. Оценить неопределенность в энергии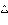 
E испущенного 
-кванта.
Решение.
Из соотношения неопределенностей Гейзенберга получим
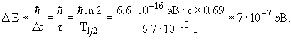
где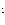 
-среднее время жизни возбужденного состояния.
Рассчитать длины волн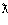 
протона и электрона с кинетической энергией T = 10 МэВ.
Решение.
Протон нерелятивистский (Tp << mpc2). В этом случае
,
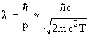учитывая, что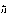 
c = 197 МэВ·Фм, имеем
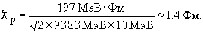
Электрон релятивистский (Te >> mec2). В этом случае
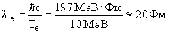
Протон, электрон и фотон имеют одинаковую длину волны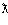 
= 10-
9 см. Какое время t им необходимо для пролета расстояния L = 10 м?
Решение.
Для протона и электрона:
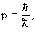
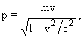
т.е.
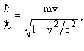
откуда получаем, что
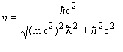
Время пролета
.
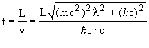Протон: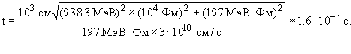 
Электрон: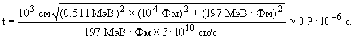 
Фотон: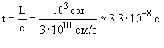 
Задача 7.
Длина волны фотона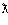 
= 3·10-11см. Вычислить импульс p фотона.
Решение.
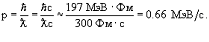
Задачи для самостоятельного решения:
1. Пользуясь таблицей масс атомов, вычислить удельную энергию связи для ядер 2Не3, 2Не4.Какой из этих изотопов является более устойчивым?
2. Вычислить минимальную энергию, необходимую для удаления одного нейтрона из ядра 7N14.
3. Вычислить массы ионов лития 3Li7— однозарядного, двухзарядного и трехзарядного (ядра лития)
4. Химический элемент кислород представляет собой смесь трех изотопов:
8О16, 8О17, 8О18,
массы которых в у. е. соответственно равны
15,99491, 16,99913, 17,99916,
а распространённость
99,759%, 0,037%, 0,204%.
Вычислить по этим данным относительную атомную массу (атомный вес) элемента кислорода.
