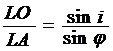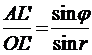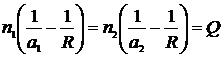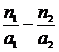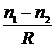Понятие оптического изображения. Преломление и отражение света на сферической поверхности

Преломление и отражение света на сферической поверхности.

Предположим, что две среды с показателями преломления n₁ и n₂ разделяются сферической поверхностью Σ (рис. 3.2.). На ли­нии LL', проходящей через центр нашей сферы О, поместим точечный источник света L. Рассмотрим узкий гомо­центрический конус лучей, падающий из L на поверх­ность раздела двух сред.

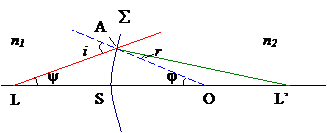
Рис. 3.2. Преломление параксиальных лучей на сферической границе двух сред.

Мы предполагаем пучок настолько узким, т.е. угол настолько малым, что практи­чески можно считать отрезок LS равным LA, L'S равным L'A и т.д. Такой узкий пучок будем называть параксиальным. Итак, условие параксиальности пучка есть

LS » LA и  L'S » L'A.

Возьмем какой-либо луч из этого пучка, например LA, падающий на Σ под углом i, построим сопряженный ему преломленный луч AL' (угол преломления r) и найдем положение точки, в которой преломленный луч пересечет ось системы.

Из треугольника ALO имеем

,

из треугольника OAL'

.

Отсюда

(1)

В дальнейшем все отрезки вдоль оси будем отсчитывать от точки S, считая положительными отрезки, откладываемые от S вправо (в направлении распространяющегося света), и отрицательными - отрезки, откладываемые влево.Таким образом,  AL » SL= - а_{1 ,} AL'» SL'= а₂,  AO = SO = R (радиус нашей сферы). В таком случае LO = -а₁ + R, OL' = а₂ - R. Используя закон преломления при переходе из первой среды во вторую, получим

=;

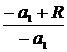
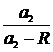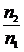т.е.

(2)

Последняя формула показывает, что произведение 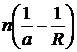 при преломлении сохраняет свою величину Q. Его называют нулевым инвариантом Аббе. Для многих целей этой формуле удобно придать вид

= (3)

Соотношение (3) позволяет найти длину а₂ = SL', если за­дано а₁ = LS, т.е. позволяет отыскать положение точки L' по за­данному L. При выводе его мы, кроме закона преломления, поль­зовались еще допущением, что луч LA принадлежит к параксиаль­ному пучку. Следовательно, соотношение справедливо для любого луча параксиального пучка. Из формулы (3) видно, что а₂ при заданных параметрах задачи (п₁, n₂, R) зависит только от а₁. Таким образом, все лучи параксиального гомоцентрического пучка, выходящего из L, пересекают ось в одной и той же точке L', которая является, следовательно, стигматическим изображением источника L. Итак, гомоцентрический пучок при преломлении на сферической поверхности остается гомоцентрическим, если он удовлетворяет условию параксиальности. Основное уравнение (3) охватывает все случаи преломления лучей на сферической поверхности. Поль­зуясь установленным выше правилом знаков, мы можем разобрать случай выпуклой (R>0) или вогнутой (R < 0) поверхности.

Точно так же в зависимости от того, будут ли а₁ и a₂ иметь разные знаки или одинаковые, мы будем иметь случаи, когда изображение располагается с противоположной по сравнению с источником сто­роны преломляющей поверхности или лежит по одну сторону с ним. В первом случае (а₂ > 0) точка, именуемая изображением, есть действительно точка пересечения преломленных лучей. Такое изо­бражение называется действительным. Во втором случае (а₂ < 0), очевидно, преломленные лучи, идущие во второй среде, остаются расходящимися и реально не пересекаются. В этом случае название изображения относится к той воображаемой точке, которая пред­ставляет собой место пересечения предполагаемого продолжения преломленных лучей. Такое изображение называется мнимым. Наши рассуждения и формула (3) показывают, что гомоцентри­ческий пучок после преломления направлен так, что его лучи или пересекаются в одной точке (действительное изображение), или мо­гут быть представлены как пересекающиеся в одной точке (мнимое изображение). Именно в этом смысле он и остается гомоцентрическим. Так как для всех наших рассуждений нам важно знать направление световых лучей, то при всех построениях мы одинаково можем пользоваться как действительным, так и мнимым изображением.

Формула (3) показывает также, что если бы источник был в L', то изображение расположилось бы в L (взаимность).