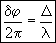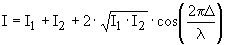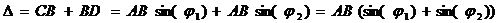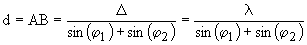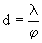Общие сведения об интерференции
Интерференция света
Интерференция света — это сложение полей световых волн от двух или нескольких (сравнительно небольшого числа) источников. В общем случае поляризация каждой из интерферирующих волн (т. е. направление, вдоль которого колеблется вектор электрического поля; магнитное поле не учитываем) имеет свое направление, и сложение двух волн есть векторное сложение. Обычно рассматривают интерференцию волн, имеющих одинаковую поляризацию. Тогда волны складываются алгебраически.
Пусть имеются два источника гармонических электромагнитных волн, создающих на некотором отдалении от себя в точке наблюдения поля, колеблющиеся следующим образом:
E1(t) = E1 cos(wt + j1),
E2(t) = E2 cos(wt + j2 ).
Здесь Е1 и Е2 — амплитуды колебаний (происходящих с одинаковой частотой); j1 и j2 — их фазы. Для простоты положим
E1 = E2 = E0. Тогда результирующее колебание имеет вид:
E=2E0 cos1/2(j1 - j2)cos[ wt + +1/2(j1 + j2 )] = ER cos(wt + jR).
Следовательно, результирующее колебание есть также синусоидальное колебание, но с иными амплитудой и фазой:
ER = 2E0 cos1/2(j1 - j2), jR= 1/2(j1 + j2).
Результирующее поле имеет амплитуду, связанную с амплитудами соотношением
E2R = E21 + E22 + 2E1E2cos(j2 — j1).
Как известно, интенсивность электромагнитной волны, проходящей через некоторую точку пространства, пропорциональна квадрату напряженности электрического поля в этой точке. Следовательно, суммарная интенсивность света в точке наблюдения складывается из интенсивности обоих источников E21 и E22 и дополнительного фактора, который можно назвать интерференционным членом: 2E1E2 cos(j2 — j1).
В зависимости от разности фаз j2 — j1 колебаний источников он может быть положительным, отрицательным или равным нулю. При этом предполагается, что j2 — j1 не зависит от времени, а только от пространственных координат. Источники, удовлетворяющие этому условию, называются когерентными.
Оптическая разность хода
Вместо разности фаз δφ интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину Δ — оптическую разность хода, которая отличается множителем λ/2π, где λ- длина световой волны.
Изменению разности фаз на 2π соответствует изменение разности хода на λ.
В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. В соответствии соотношением вместо реального уменьшения длины волны λ можно рассматривать неизменную λ и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в n раз больше геометрической длины. Далее, употребляя термин «разность хода», всегда будем иметь в виду оптическую разность хода.
Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:
.
Ширина интерференционных полос
Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.
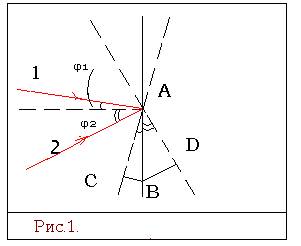Пусть две плоские световые волны падают на экран под углами φ1 и φ2 (рис.1), точки А и В — середины двух соседних светлых полос на экране, АС- поверхность равной фазы первой волны, АD- поверхность равной фазы второй волны. Поверхность AC имеет ту же фазу, что и поверхность AD, так как в точке A фазы двух волн одинаковые (светлая полоса). Поэтому можно считать, что это одна и та же поверхность равной фазы волны, идущей от одного точечного источника разными путями. Следовательно, оптическую разность хода, например для точки экрана B, можно отсчитывать от пары точек C и D как бы общей поверхности равной фазы.
Из рис.1 видно, что поверхность равной фазы AC первой волны еще не дошла до точки B на отрезок CB, а поверхность AD второй волны уже зашла за точку B на отрезок BD. Тогда оптическая разность хода Δ для точки B равна
.
Точки A и B — середины соседних светлых полос, тогда оптическая разность хода равна длине волны Δ=λ, так как при переходе по экрану на одну полосу разность хода меняется на λ. Выражая из этого равенства ширину полосы AB, и обозначая ее через d, получаем
,
где знак «+» соответствует положительным углам падения φ1 и φ2 отсчитанным в разные стороны от нормали к экрану, как на рис. 1.
В большинстве задач углы падения малы, тогда sin(φ)≈φ и выражение для ширины полос упрощается
,
где φ=φ1+φ2 — угол между лучами сходящимися на экране.
