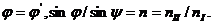Фазовые соотношения между падающей, отраженной и преломленной волнами на границе раздела сред

Рассмотрим задачу о прохождении электромагнитной волны через плоскую границу двух диэлектрических сред I и II (одной из них может, в частности ,быть и вакуум). Эта ситуация представлена на рисунке 2.6.1(а), (б) для случая двух различных поляризаций . Направление электрического и магнитного векторов соответствует правилу, согласно которому k, E, B образуют правую тройку. Мы использовали в качестве магнитного вектора H, поскольку именно для него будем писать соответствующее граничное условие. Заметим, что магнитное поле ориентированно на рис. 2.6.1(а) так же, как электрическое поле на рис. 2.6.1(б) ( с точностью до знака), а на рис. 2.6.1(б) — ортогонально плоскости рисунка. Результаты которые мы получили, можно переносить и на случай искривленной поверхности раздела. Она лишь должна быть гладкой, а радиус кривизны ее должен  многократно превосходить характерный пространственный масштаб электромагнитного поля — длину волны. Т.о. мы опишем действие на электромагнитную волну , в частности , поверхности линзы. Все расчеты линз, тонких и толстых, а также и сложных оптических систем базируются именно на законе преломления . Мы будем пользоваться не понятием луча, принятым в геометрической оптике, а более корректным с точки зрения электродинамики понятием волнового фронта; «лучи»- падающий, отраженный и преломленный — изображенные на рис.2.6.1, представляют в наших терминах нормали к волновому фронту, направление которых задается вектором k.

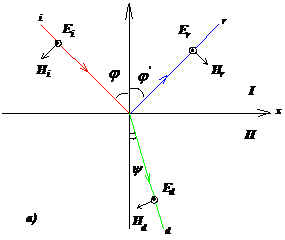
2.6.1 (а) Падающий, отраженный и преломленный лучи

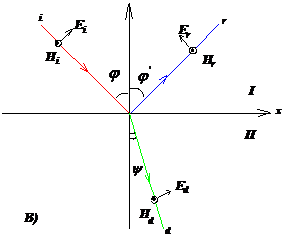
2.6.1 (б) Падающий, отраженный и преломленный лучи

Пусть показатели преломления сред I и II равны , соответственно 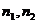( в вакууме просто единице ). Мы показали на каждом из рисунков 2.6.1 три волны : падающую (i), отраженную (r) , и преломленную (d).  Это экспериментальный факт , известный каждому школьнику, но даже не зная этого заранее , можно было бы его предсказать , исходя из уравнений Максвелла. В случае падения электромагнитной волны на проводящую поверхность у нас «работало» единственное нетривиальное граничное условие — закон сохранения тангенциальной компоненты электрического поля , а все остальные выполнялись должным образом за счет зарядов и токов , индуцированных на поверхности проводника Теперь такой возможности нет , так как  мы имеем с диэлектрическими средами , а поэтому всего лишь одной волны помимо падающей, нам просто не хватит. В каждой из двух ситуаций на рис. 2.6.1 нам придется выполнять условие непрерывности  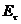и . 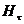Третье условие -  сохранение  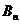в случае , изображенном на рис. 2.6.1 (а), и  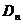в случае рис. 2.6.1(б) — -будет выполнено автоматически как следствие закона преломления.

Еще один вопрос , на который целесообразно ответить заранее: правомерно ли разделение постановки задачи именно на те два случая , которые представлены на рис. 2.6.1(а) и (б)? Не могут ли возникнуть отраженные либо преломленные волны с поляризацией , ортогональной таковой в падающей волне? Ответ: не могут , и это прямое следствие уравнений Максвелла и граничных условий . В силу линейности задачи, мы можем расщепить решение уравнений Максвелла на два линейно независимых , соответствующих двум различным поляризациям . Выбирая решение с одной из поляризаций — той же что и падающей волны, мы оперируем с полями трех волн, что позволяет выполнить граничные условия 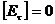,  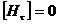или 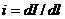. При попытки выполнить их для другой поляризации нам опять не хватит переменных , т.к. в нашем распоряжении будет только две волны, без падающей, так что единственным возможным решением  с такой поляризацией окажется нулевое поле. Разумеется, эти рассуждения находятся в полном с экспериментальными данными. Пусть все три волны записаны в виде  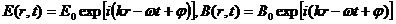 .       (2.6.1)

Очевидно , для линейной среды зависимость H(r,t) или B(r,t) будет иметь точно такой же вид. Воспользуемся для случая ( а ) граничным условием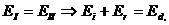

а для случая (б)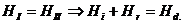                  

(мы учли, что в обоих случаях в соотношение входят параллельные векторы). Поскольку дальнейшие действия для обеих поляризаций совершенно идентичны , мы ограничимся случаем рис.2.6.1 (а). Пусть в какой тог момент граничное условие выполнено. Однако оно сразу же нарушится , если зависимость от времени не будет одинаковой для всех трех полей . Это означает , что частота всех трех волн должна быть одинаковой ( и действительно , отражение от прозрачной среды  и преломление в ней « сохраняют цвет»). Далее введем в плоскости падения вдоль границы сред координату x . Из поперечности волн  и паралельности векторов 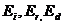 следует, что все три волновых вектора  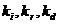лежат в одной плоскости — падения. Вдоль оси Ox произведения kr  в формулах типа (2.6.1) вырождаются в 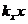. Т.о. , граничное условие при равных частотах сводится к следующему :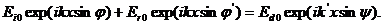

Мы воспользовались обозначением углов рис.2.6.1 и учли, что из равенства частот для падающей и отраженной волн следует равенство волновых чисел. Для преломленной волны волновое число 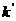 определяется формулой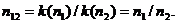

Теперь потребуем, чтобы наше граничное условие выполнилось в любой точке оси Ox. Для этого необходимо, чтобы экспоненциальные множители были тождественно равны друг другу, а значит, равны должны быть и их аргументы:

.

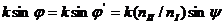Мы получили аналитически  из законов электродинамики хорошо известные правила вычисления углов отражения и преломления: