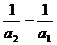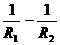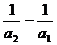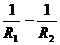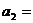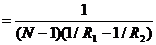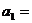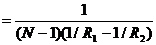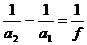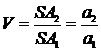Сферические зеркала и тонкие линзы
А. Фокусы сферической поверхности
Из основного уравнения (1.3)
следует, что
при a1 = -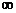
при а2= 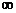
т.е. f1, f2 зависят только от радиуса кривизны поверхности R и показателей преломления n1, n2 обеих сред.
Величины f1 и f2 суть постоянные длины, характеризующие преломляющую поверхность. Они называются ее фокусными расстояниями: f1 - переднее фокусное расстояние (точка F1 - передний фокус); f2 - заднее фокусное расстояние (точка F2 - задний фокус) (рис. 3.3).
Таким образом, фокусом сферической поверхности называется точка, в которой сходятся после преломления параллельные лучи (т. е. лучи, идущие из бесконечно удаленной точки). Понятно, что фокусы, также как и изображения, могут быть действительными и мнимыми, т. е. представлять точку пересечения преломленных лучей (бывших до преломления параллельными) или их предполагаемых продолжений. Так, если вогнутая сторона поверхности раздела обращена к среде, имеющей меньший показатель преломления, то оба фокуса будут мнимыми. В этом легко убедиться как из анализа формул (1) и (2), так и из построения.
Параллельные лучи, идущие справа налево вдоль NO (см. рис. 3.3), сойдутся в фокусе 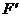 1, расположенном на линии NO и лежащем также на расстоянии
1, расположенном на линии NO и лежащем также на расстоянии  от преломляющей поверхности. Геометрическое место точек Fl
от преломляющей поверхности. Геометрическое место точек Fl 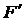 1... образует сферическую поверхность с радиусом
1... образует сферическую поверхность с радиусом 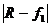 (для случая, показанного на рис. 3.3, f1 > 0), концентрическую с преломляющей сферой (с центром в точке О).
(для случая, показанного на рис. 3.3, f1 > 0), концентрическую с преломляющей сферой (с центром в точке О).
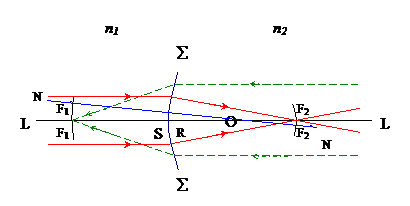 Рис. 3.3. Фокусы сферической поверхности
Рис. 3.3. Фокусы сферической поверхности
Эта поверхность носит название передней фокальной поверхности. Аналогично построим заднюю фокальную поверхность радиуса 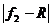 . Малые участки этих поверхностей (для параксиальной области) могут быть приняты за плоскости (фокальные плоскости). Фокусные расстояния сферической поверхности различны по знаку и не равны между собой по абсолютной величине (см. рис. 3.3), ибо n1
. Малые участки этих поверхностей (для параксиальной области) могут быть приняты за плоскости (фокальные плоскости). Фокусные расстояния сферической поверхности различны по знаку и не равны между собой по абсолютной величине (см. рис. 3.3), ибо n1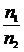 n2 Рассматриваемый случай легко осуществить на опыте, взяв широкую стеклянную трубку и заклеив один ее конец часовым стеклом, имеющим сферическую форму. Если налить в трубку воду или, еще лучше, бензол, показатель преломления которого практически совпадает с показателем преломления часового стекла, то получим сферическую границу раздела между воздухом (n1 = 1,00) и бензолом (п2 = 1,49). На этом простом аппарате легко убедиться, в согласии с (1) и (2), что
n2 Рассматриваемый случай легко осуществить на опыте, взяв широкую стеклянную трубку и заклеив один ее конец часовым стеклом, имеющим сферическую форму. Если налить в трубку воду или, еще лучше, бензол, показатель преломления которого практически совпадает с показателем преломления часового стекла, то получим сферическую границу раздела между воздухом (n1 = 1,00) и бензолом (п2 = 1,49). На этом простом аппарате легко убедиться, в согласии с (1) и (2), что
f2 / f1 = - n2 / n1 (3)
Важным практическим примером одной преломляющей сферической поверхности является система, эквивалентная глазу и носящая название «приведенный глаз». В качестве второго примера рассмотрим сферическое зеркало. Формулу (3) параграфа 3.4 можно применить и к случаю отражения, если положить n2= - n1 . Тогда имеем
1/a1 + 1/a2 = 2/R (4)
т. е. известную формулу сферического зеркала. Фокусное расстояние такого зеркала определится по формуле (1). Найдем f= R/2, и, следовательно, формуле зеркала можно придать вид
1/a1 + 1/a2 = 1/f (5)
В случае зеркала изображение действительное, если оно лежит
по одну сторону с источником, и мнимое, если расположено за зеркалом.
Случаи вогнутого и выпуклого зеркала отличаются лишь знаком R. Легко видеть, что фокус вогнутого зеркала - действительный, а фокус выпуклого зеркала - мнимый.
Чтобы получить законы плоского зеркала, достаточно положить R = 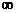 . В этом случае найдем а1 = а2, т.е. изображение точки в плоском зеркале мнимое и симметрично расположенное.
. В этом случае найдем а1 = а2, т.е. изображение точки в плоском зеркале мнимое и симметрично расположенное.
Б. Изображение малых предметов при преломлении на сферической поверхности.
Пользуясь свойствами параксиальных гомоцентрических пучков, можно построить изображение небольших площадей при преломлении на сферической поверхности. Представим себе сферическую поверхность, около центра которой расположена небольшая диафрагма DD, выделяющая узкие пучки, имеющие характер параксиальных по отношению к соответствующим осям.
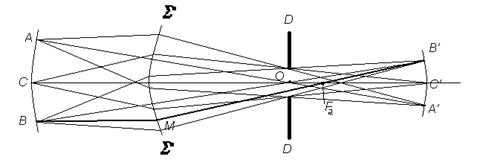 Рис. 3.4. Изображение малого предмета АСВ при преломлении на сферической поверхности.
Рис. 3.4. Изображение малого предмета АСВ при преломлении на сферической поверхности.
Параксиальный гомоцентрический пучок после преломления остается гомоцентрическим, т.е. дает изображение своей вершины. Соответствующим образом изобразится любая точка светящейся дуги АСВ (или части сферы) (рис. 3.4) с центром в О. Для отыскания изображения всех точек АСВ применим формулу
Так как для всех точек АСВ все а1 имеют одно и то же значение, то и все а2 одинаковы; элемент сферы с радиусом R-а1 отобразится в виде элемента сферы с радиусом a2-R с общим центром О. Для графического отыскания точки В', например, можно провести луч BM, параллельный СO; тогда преломленный луч должен пройти через фокус F2; луч же ВО проходит без преломления. Пересечение продолжений MF2 и ВО и определит положение В'.
Ввиду того, что АВ и А'В' очень малы, вместо дуг (элементов сферы) можно брать хорды (элементы плоскости). Таким образом, в сферической системе малая площадка, перпендикулярная к оси, изобразится при помощи параксиальных лучей в виде площадки, также перпендикулярной к той же оси.
Плоскость предмета АВ и плоскость его изображения А'В' называются плоскостями, сопряженными по отношению к данной оптической системе.
В. Увеличение. Теорема Лагранжа-Гельмгольца.
Выберем в качестве светящегося предмета линию А1В1, перпендикулярную к оси, и построим ее изображение A2В2 (рис. 3.5). Отношение линейных размеров изображения (y2 = A2В2) и предмета (y1 = A1B1) носит название линейного или поперечного увеличения
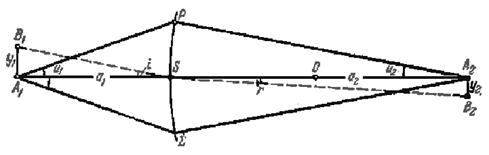 Рис. 3.5. К выводу уравнения Лагранжа-Гельмгольца для параксиальных лучей.
Рис. 3.5. К выводу уравнения Лагранжа-Гельмгольца для параксиальных лучей.
V = y2 / y1 = A2B2 / A1B1. Приписывая A1B1 и A2B2 знаки (как обычно в геометрии), получим, что увеличение положительно, если изображение прямое, и отрицательно, если изображение перевернутое. Из треугольников A1B1S и A2B2S имеем
y1/a1 = tg i, y2/a2 = tg r.
При малых размерах A1B1 и A2B2
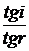 =
=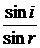 =
=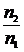
т. е.
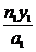 =
=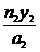 или
или 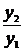 = V =
= V = 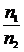
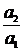 . (6)
. (6)
Для преломляющей системы n1 и n2 всегда положительны, так что знак V определится знаком отношения a2/a1. Для расположений, соответствующих действительному изображению (см. рис. 3.5), a1 и a2 имеют разные знаки, т.е. V отрицательно, и изображение перевернутое; для мнимых изображений - наоборот.
Для зеркал п1/п2 = -1, т.е. V = -а2/а1. В случае действительного изображения а1 и a2 имеют одинаковые знаки, т. е. V < 0 и изображение перевернутое; в случае мнимого изображения знаки а1 и a2 различны, V > 0, изображение прямое. Для плоского зеркала (а1= -a2) V = 1, т. е. изображение прямое и натуральной величины.
Сопряженные, плоскости называются главными, если для них V = 1, т. е. изображение получается прямым и в натуральную величину объекта. Нетрудно видеть, что для сферической поверхности главные плоскости совпадают между собой и представлены плоскостью, касательной к сфере в точке S , т.е. а1 = а2 = 0. В соответствии с этим и фокусные расстояния сферической поверхности следует считать расстояниями от главных плоскостей до фокусов. На рис. 3.5 изображены также углы и1 и u2, определяющие максимальное раскрытие (апертуру) пучков, падающих на поверхность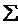 (угол 2u1), и сопряженных им изображающих пучков (угол 2u2). Предельное значение этих углов определяется требованием соблюдения условий параксиальности.
(угол 2u1), и сопряженных им изображающих пучков (угол 2u2). Предельное значение этих углов определяется требованием соблюдения условий параксиальности.
Так как при всех значениях углов и, лежащих в пределах апертуры параксиальных лучей, отношение а2/а1 остается постоянным, то соотношение (7) показывает, что увеличение небольшого предмета A1B1 сохраняется неизменным, какой бы частью параксиального пучка ни было образовано изображение. Другими словами, не только изображение точки на оси, но и изображение небольшого предмета, расположенного около оси, передается параксиальным пучком без искажения.
Для параксиальных лучей А1Р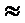 А1S = a1 и РА2
А1S = a1 и РА2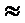 SA2 = а2, так что
SA2 = а2, так что
u1 = tg u1 = 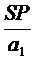 , u2 = tg u2 =
, u2 = tg u2 = 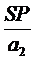 ,
,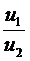 =
= 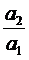 .
.
На основании (6) имеем
или
y1n1u1 = y2n2u2 (7)
Соотношение (7) носит название теоремы Лагранжа-Гельмголъца.
Это соотношение справедливо для области параксиальных лучей. При употреблении пучков со значительной апертурой получение четких изображений возможно лишь при выполнении условия
y1n1 sin u1 = y2n2 sin u2 (8)
Условие Лагранжа - Гельмгольца или условие синусов налагает ограничение на свободу преобразования световых пучков при помощи оптических систем, связывая апертуру и размер предмета с апертурой и размером изображения. Из него вытекает, что преобразование данного оптического пучка при помощи оптической системы в другой пучок любого наперед заданного строения невозможно. Строение преобразованного пучка может быть только таким, какое допускает условие Лагранжа-Гельмгольца. Это важное принципиальное ограничение приобретает особое значение в вопросах фотометрии и концентрирования лучистой энергии при помощи оптических систем.
Г. Преломление в линзе
Общая формула линзы
Общая формула линзы
Большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал (обычно стекло) от окружающего воздуха. Такая система представляет, очевидно, обычную линзу.
Линза называется тонкой, если обе ее вершины можно считать совпадающими, т.е. если толщина линзы d мала по сравнению с R1 и R2, радиусами кривизны ограничивающих поверхностей. На рис. 3.6 для ясности линза изображена толстой. В дальнейших расчетах будем полагать, что точки S1 и S2 сливаются, и обозначим их буквой S. Все расстояния будем отсчитывать от этой точки S, которая практически совпадает с S1 и S2. Точка S носит название оптического центра линзы. Любой параксиальный луч, проходящий через S, практически не испытывает преломления. Действительно, для таких лучей участки обеих поверхностей линзы можно считать параллельными, так что луч, проходя через них, не меняет направления, но лишь смещается параллельно самому себе (преломление в плоскопараллельной пластинке), а так как толщиной линзы мы пренебрегаем, то смещение это ничтожно и луч практически проходит без преломления. Луч, проходящий через оптический центр, мы назовем осью линзы. Та из осей, которая проходит через центры обеих поверхностей, называется главной, остальные - побочными.
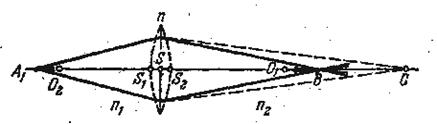 Рис. 3.6. Преломление в тонкой линзе
Рис. 3.6. Преломление в тонкой линзе
Преломление на первой сферической поверхности создало бы без второй сферической поверхности в сплошном стекле с показателем преломления п изображение С на, расстоянии SC = а (см. рис. 3.6) от вершины, так что
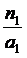 =
=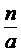 =
= 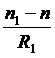 ,
,
где a1 = SA1 , R1 - радиус кривизны первой поверхности линзы. Для второй поверхности С является как бы мнимым источником света. Построение изображения этого источника после преломления на второй поверхности линзы даст точку В на расстоянии a2 = SB от линзы. Здесь опять применима формула
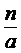 =
= 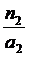 =
= 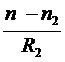 ,
,
где R2 - радиус второй поверхности.
Так как n1 = n2 (воздух с двух сторон линзы), то имеем:
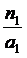 =
=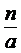 =
= 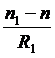 ,
,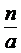 =
=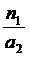 =
= 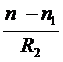 ,
,
Складывая второе уравнение с первым, получим:
или, вводя относительный показатель преломления N = n/n1 ,
Эта общая формула линзы годна для линз выпуклых и вогнутых при любом расположении источника и соответствующем расположении фокуса. Нужно только принять во внимание знаки а1, a2, R1, R2 считая их положительными, если они отложены вправо от линзы, и отрицательными, если они отложены влево от линзы (как было сделано при выводе формулы (2) в параграфе 3.4). Если знаки а1 и a2 одинаковы, то одна из сопряженных точек - мнимая, т. е. в ней пересекаются не сами лучи, а их воображаемые продолжения.
Д. Фокусные расстояния тонкой линзы.
Если светящаяся точка, лежащая на главной оси, удаляется от линзы (а1 возрастает по абсолютной величине), то изображение перемещается. Положение изображения, соответствующее предельному случаю, когда источник удален в бесконечность, носит название фокуса линзы.
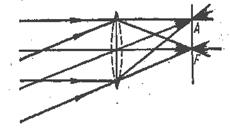 Рис. 3.7. Положение фокусов, расположенных на главной и побочной оптических осях. AF - фокальная плоскость линзы.
Рис. 3.7. Положение фокусов, расположенных на главной и побочной оптических осях. AF - фокальная плоскость линзы.
Таким образом, фокус есть точка, сопряженная бесконечно удаленной точке главной оси, или, что то же, - место схождения лучей, параллельных главной оптической оси. Расстояние от линзы до фокуса есть фокусное расстояние тонкой линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси, называется фокальной плоскостью.
Если лучи идут из бесконечности параллельным пучком, но под углом к главной, оси (вдоль побочной оси), то они пересекаются в соответствующей точке А фокальной плоскости (рис. 3.7). Таким образом, фокальная плоскость есть плоскость, сопряженная бесконечно удаленной плоскости.
Для определения фокусных расстояний имеем следующие соотношений;
при а1 = - 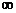
при a2 = 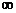
т.е.
f1 = - f2 (12)
Итак, фокусные расстояния линзы равны по величине и противоположны по знаку, т.е. фокусы лежат по разные стороны от линзы.
В зависимости от знака и величины R1 и R2 , а также от знака (N-1), величина f1 может быть положительной либо отрицательной, т.е. фокус может быть мнимым или действительным. То же относится и к f2 , причем нетрудно видеть, что если первый фокус - мнимый, то и второй будет мнимым, и наоборот.
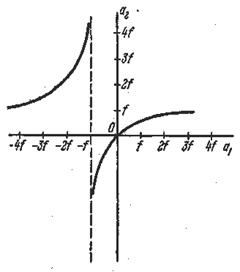 Рис. 3.9. Графическая зависимость между а1 и а2 при данном f для идеальной тонкой линзы.
Рис. 3.9. Графическая зависимость между а1 и а2 при данном f для идеальной тонкой линзы.
Если фокусы действительны, т.е. параллельные лучи после преломления в линзе сходятся, то линза называется собирательной или положительной. При мнимых фокусах параллельные лучи после преломления в линзе становятся расходящимися. Поэтому такие линзы называются рассеивающими или отрицательными.
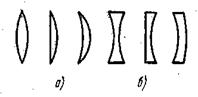 Рис. 3.8. Различные типы тонких линз. а - собирательные, б - рассеивающие.
Рис. 3.8. Различные типы тонких линз. а - собирательные, б - рассеивающие.
Если материал тонкой линзы преломляет сильнее, чем окружающая среда (например, стеклянная линза в воздухе), то собирательными будут линзы двояковыпуклые, плоско-выпуклые и вогнуто-выпуклые (положительный мениск), т. е. линзы, утолщающиеся к середине (рис. 3.8, а); к рассеивающим линзам принадлежат двояковогнутые, плоско-вогнутые и выпукло-вогнутые (отрицательный мениск), т, е. линзы, утончающиеся к середине (см. рис. 3.8, б). Если материал тонкой линзы преломляет меньше, чем окружающая среда (например, воздушная полость в воде), то линзы, вида рис. 3.8, а будут рассеивающими, а вида рис. 3.8, б - собирательными.
Вводя фокусное расстояние линзы, придадим формуле линзы вид
Зависимость между а1 и а2 графически изображена на рис. 3.9. Легко видеть, что изменение величины а1 приводит к изменению a2 того же знака. Другими словами, изображение сдвигается вдоль оси в том же направлении, что и объект. Исключение составляет лишь точка а1= f1 при прохождении которой изображение переходит из a2 = +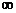 в a2 = -
в a2 = - 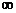 .
.
Е. Изображение в тонкой линзе. Увеличение.
Пусть малый объект вблизи оси изображается системой центрированных сферических поверхностей. Построение можно выполнить при помощи параксиальных пучков (см. п. Б.). Поскольку доказано, что дли параксиальных лучей изображение точки стигматично (т.е. гомоцентричность пучка сохраняется), то для построения ее изображения достаточно найти точку пересечения каких-либо двух лучей.
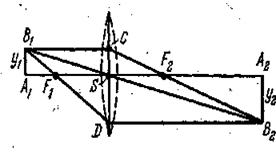 Рис. 3.10. Построение изображения в тонкой линзе
Рис. 3.10. Построение изображения в тонкой линзе
Наиболее простое построение выполняется при помощи лучей, указанных на рис. 3.10. Один из них - луч CF2B2, сопряженный с лучом B1C, параллельным главной оптической оси; этот луч походит через задний фокус F2; другой - луч DB2, параллельный главной оптической оси и сопряженный с лучом B1F1D , проведенным через передний фокус F1. Третий луч вдоль побочной оптической оси B1SB2 проходит через оптический центр линзы (точку S), - он идет, не преломляясь. Построение этих лучей выполняется без затруднений. Всякий другой луч, идущий из В1, нужно было бы строить при помощи закона преломления, что гораздо сложнее. Но из свойства гомоцентричности следует, что после выполнения построения любой преломленный луч пройдет через точку В2. Так как построение изображения точки В1 сводится к геометрической задаче отыскания точки В2, то нет надобности, чтобы выбранные простейшие пары лучей имели реальный характер. В частности, когда A1B1 больше размеров линзы (например, фотографирование), лучи В1С, B1D (рис. 3.11) не проходят через линзу, но могут быть использованы для построения изображения. Реальные лучи, участвующие в построении изображения, ограничены оправой линзы MN, но сходятся, конечно, в той же точке В2, ибо линза предполагается, достаточно хорошей, так что проходящие через нее пучки остаются гомоцентрическими.
Определив поперечное увеличение, как и в п. В, при помощи соотношения 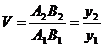 , найдем из рис. 3.10.
, найдем из рис. 3.10.
Аналогично изложенному в п. В найдем, что для действительных изображений V<0, т. е. изображение обратное, а для мнимых V>0, т.е. изображение прямое.
Главными плоскостями линзы, как и всякой системы, являются те сопряженные плоскости, для которых V=1. Для тонкой линзы эти плоскости сливаются в одну, проходящую через оптический центр перпендикулярно к оптической оси (т.е. а1=а2=0). Таким образом,
фокусные расстояния линзы, которые должны отсчитываться от главных плоскостей, в случае тонкой линзы могут отсчитываться от ее поверхности.
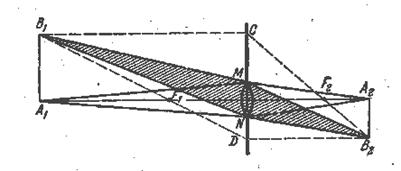 Рис. 3.11. Ограничение пучков в тонкой линзе.
Рис. 3.11. Ограничение пучков в тонкой линзе.
Тонкая линза как система двух центри-рованных поверхнос-тей представляет про-стейшую оптическую систему, дающую до-вольно несовершен-ное изображение. В большинстве случаев мы прибегаем к построению более сложных систем, характеризующихся наличием большого числа преломляющих поверхностей и не ограниченных требованием близости этих поверхностей (тонкости линзы). Однако даже простые тонкие линзы имеют очень большое значение на практике, главным образом в качестве очковых стекол. В громадном большинстве случаев очки представляют собой просто тонкие линзы.
Для классификации очковых, стекол обычно применяется понятие оптической силы линзы. Оптической силой называется величина, обратная заднему фокусному расстоянию линзы. Если фокусное расстояние измерять в метрах, то оптическую силу принято выражать в диоптриях, считая ее положительной или отрицательной, в зависимости от того, собирательная линза или рассеивающая. Так, например, рассеивающая линза с фокусным расстоянием 20 см (f=-1/5 м) имеет оптическую силу в - 5 диоптрий.
Ж. Каустическая поверхность. Характер ее симметрии.
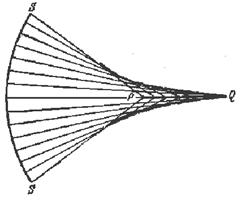
Поверхность, огибающая совокупность лучей преломленного пучка, носит название каустической поверхности (каустики), а ее сечение любой плоскостью, проходящей через луч, - каустической кривой. Если пучок при прохождении через оптическую систему сохранил гомоцентричность, то каустика вырождается в точку, представляющую вершину гомоцентрического пучка. Нарушение гомоцентричности означает большее или меньшее искажение каустической поверхности по сравнению с этим простейшим вырожденным случаем. Можно классифицировать различные аберрации по характеру понижения симметрии каустической поверхности. Так, при сферической аберрации каустика приобретает вид поверхности, обладающей осью симметрии, но не имеющей центра симметрии. Рис. 3.12. изображает одну из таких форм, где жирные линии
Рис. 3.12. Сечение каустической поверхности.
SS - волновой фронт.представляют каустическую кривую в плоскости рисунка, а сама каустика получается вращением рисунка относительно оси PQ. Аберрация астигматизма соответствует дальнейшему понижению симметрии каустической поверхности, которая не имеет больше оси симметрии, а обладает лишь двумя взаимно перпендикулярными плоскостями симметрии.
Аберрация комы означает, что каустическая поверхность обладает лишь одной плоскостью симметрии, проходящей через светящуюся точку и оптическую ось.
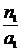
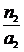
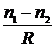
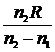
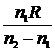
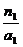
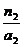
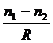
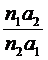
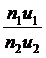
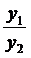
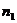 (
(