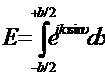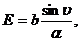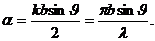Дифракция Фраунгофера на щели

Простейшим для расчета и практически очень важным случаем является фраунгоферова дифракция на длинной прямоугольной щели (Дифракция Фраунгофера на щели). Ширину щели обозначим через b, ее длину будем считать бесконечной. Пусть на щель нормально падает плоская монохроматическая волна (рис. 5.7.1). Световое поле за щелью найдется по принципу Гюйгенса как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели. Вторичные волны, излучаемые полоской волнового фронта ширины dx, параллельной щели, складываясь, дают цилиндрическую волну, осью которой является эта полоска. Зависимость этой волны от направления ее распространения, определяемого углом j должен предполагаться малым. Однако необходимо учесть разности фаз между волнами, исходящими из различных полосок. Разумеется, речь идет о фазах колебаний на бесконечном расстоянии от щели. Волна, исходящая из dx под углом j, опережает по фазе волну того же направления, исходящую из середины щели О, на kx sinj.

Поэтому результирующее поле в бесконечности, создаваемое всей щелью, представиться интегралом

Здесь опущены все множители, не являющиеся на относительное распределение волнового поля по направлениям. Вычислив интеграл, получим

Где введено обозначение

Отсюда для распределения интенсивности света по направлениям найдем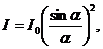

Где 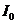- интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При 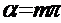, где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами.

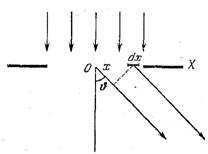
Рис. 5.7.1. Дифракция Фраунгофера на щели