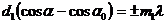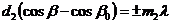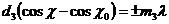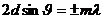Условия Лауэ. Дифракция рентгеновских лучей. Формула Брега-Вульфа

Пусть две дифракционные решетки поставлены одна за другой так, что их штрихи взаимно перпендикулярны. Такая пластинка представляет собой двумерную периодическую структуру.

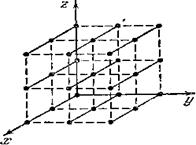
Рис. 5.11.1 Двумерная периодическая структура

Дифракция наблюдается также на трехмерных структурах, т. е. пространственных образованиях, обнаружи­вающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами яв­ляются все кристаллические тела. Однако период их (~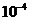мк) слишком мал для того, чтобы можно было наблюдать дифракцию в види­мом свете. Условие 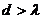, выполняется в случае кристаллов лишь для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ.

Найдем условия образования дифракционных максимумов от трехмерной структуры. Проведем в направлениях, по которым свойства структуры обнаруживают периодичность, координатные оси x, y, z (рис. 5.11.1). Структуру можно представить как совокупность равноотстоящих параллельных линейных цепочек из структурных элементов, расположенных вдоль одной из координатных осей . Рассмотрим действие отдельной линейной цепочки , параллельной , например ,  оси  х (рис. 5.11.2). Пусть на нее падает пучок параллельных лучей , образующих с осью  х угол 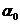.Каждый структурный элемент является источником вторичных волн. 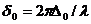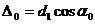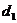К соседним источникам падающая волна приходит с разностью фаз ,где   ( — период структуры вдоль оси х ). Кроме того между вторичными волнами , распространяющихся в направлениях, образующих с осью х угол  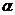( все такие направления лежат вдоль образующих конуса, осью которого служит ось х ), возникает дополнительная разность хода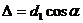

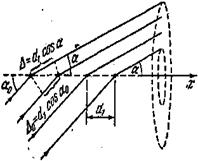
Рис. 5.11.2 Дифракция рентгеновских лучей

Под действием рентгеновского излучения каждый атом кристаллической решетки становится источником сферических волн той же частоты, что и падающих волн.
Запишем условия Лауэ
.,
.,
,
-угол между падающим пучком и осью y, -угол, образуемый с осью y направлениями, вдоль которых получаются дифракционные максимумы.
Уравнения  носят название формул Лауэ. Каждому определяемому этими уравнениями направлению(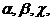) соответствуют три целочисленных индекса  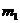и 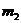 ,  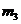. При рассмотрении дифракции от трехмерной структуры мы не касались вопроса о том, каким образом лучи, идущие от различных  структурных элементов, сводятся в одну точку экрана. В случае дифракции, наблюдаемой в видимом свете, это, как мы знаем, достигается с помощью линзы, в фокальной плоскости которой расположен экран..
Русский ученый Ю. В. Вульф и английские физики У. Г. и У. Л. Брэгги показали независимо друг от друга, что расчет дифракционной картины от кристаллической решетки можно провести также следующим простым способом.

Формула Брега-Вульфа

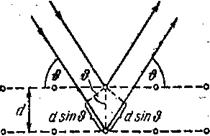
Рис. 5.11.3 Формула Брега-Вульфа

Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.5.11.3.). В дальнейшем мы будем называть их атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычным законам отражения. Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различ­ными щелями дифракционной решетки. При этом, как и  в случае решетки, вторичные волны  будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной 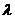.  Из рис. 5.11.3  видно, что разность хода двух волн, отразившихся от соседних атомных слоев, равна 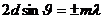,  где d — период идентичности кристалла в направлении, перпендикулярном к рассматриваемым  слоям, 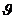- угол, дополнительный к углу падения и называемый углом скольжения падающих лучей. Следовательно, направления, в которых получаются дифракционные максимумы, определяются условием:

Соотношение называется формулой Вульфа — Брэгга.

Заметим, что расчет по формулам Лауэ и расчет по формуле Вульфа — Брэгга приводят к совпадающим результатам.