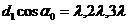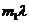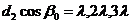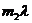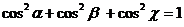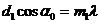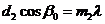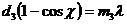Критерий наблюдения различных видов дифракции

Дифракция на многомерных структурах

Дифракционная решетка как одномерная структура

Любая функция времени может быть представлена как совокупность синусоидальных функций времени с различными периодами, амплитудами и фазами. Аналогично, любую пространственную структуру, свойства которой, например коэффициент пропускания, есть функция пространственных координат, можно представить как совокупность синусоидальных структур (теорема Фурье). В частности, если коэффициент пропускания структуры зависит только от одной координаты, например х, то коэффициент пропускания отдельных синусоидальных структур представится в виде 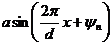где а- амплитуда, d — пространственный период и Ψ — фаза. Непериодическая структура представляется совокупностью синусоидальных структур с непрерывно меняющимся периодом (представление в виде интеграла Фурье). Периодическая структура с периодом d. представится в виде суммы членов ряда, один из которых в общем случае может быть постоянной величиной, а остальные — синусоидальными функциями х с периодом, равным 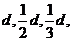…, т. е. остальные члены будут вида 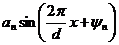,        где n=1, 2, 3,..

Характер рассматриваемой структуры определяет значения амплитуд и фаз отдельных синусоидальных членов ряда. Таким образом, дифракцию на сложной структуре можно рассчитать путем рассмотрения дифракции на каждой отдельной компоненте разложения Фурье этой структуры. Постоянный член разложения Фурье дает нулевой максимум, каждый из синусоидальных членов — по два максимума первых порядков (т = ±1). Так как периоды синусоидальных структур различны, то и углы дифракции соответствующих максимумов первого порядка будут различны, и в совокупности получится полная дифракционная картина всей структуры. Например, максимумы третьего порядка (т = ±3) суть максимум первого порядка (т = ±1) на третьей синусоидальной структуре, период которой равен 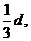. Таким образом, для изученной нами одномерной решетки (решетка с коэффициентом пропускания меняющимся только вдоль одной координаты).

Дифракция на двумерных структурах

Гораздо шире распространен случай, когда коэффициент про пускания пластинки, располагаемой в световом пучке, меняет не вдоль одного направления, а по всей поверхности нашей пластинки. Примером может служить пластинка беспорядочно запыленного стекла или окно, покрытое узорами мороза. Ясно, что такое изменение коэффициента пропускания можно охарактеризовать как изменение по двум координатам нашей поверхности, так что рассматриваемая структура будет двумерной. В простейшем случае это будет двумерная периодическая структура (двумерная решетка), в общем — совокупность многих двумерных решеток.

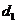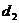Рассмотрим двумерную решетку, представляющую собой скрещенные перпендикулярные решетки с периодами и . Подобный случай легко осуществить, поставив непосредственно одну за другой две обыкновенные нарезанные на стеклянных пластинках дифракционные решетки, штрихи которых направлены перпендикулярно друг к другу. Узкий пучок монохроматического света, пройдя через первую решетку с вертикальными штрихами,, должен дать совокупное максимумов (нулевой и максимумы высших порядков) вдоль горизонтальной линии. Световой пучок, соответствующий каждому максимуму, проходя, через  вторую решетку, распадается на новую совокупность световых  пучков, дающих максимумы вдоль вертикальной линии. Пусть свет падает на подобную решетку нормально. Выберем направление света  за  ось Z,   направления  вдоль  решеток — оси X и У, охарактеризуем направления падающего пучка углами  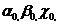дифрагировавшего — углами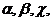. В  нашем случае 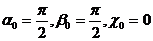, т.е., 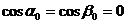,,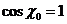 Отклонение дифрагировавшего луча вдоль X приведет к образованию минимумов и максимумов света в зависимости от величины угла дифракции. Применяя теорию одномерной решетки, мы найдем, что положения главных максимумов должны удовлетворять условиям.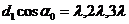

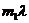
Аналогично дифракция в направлении оси У дает главные максимумы в направлениях , определяемых условиями:

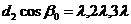
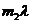Таким образом, из трех условий:

,

 

где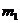 и 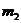— целые числа, мы определяем для заданной структуры и для данной длины волны Если решетки с периодам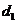и  и 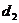не взаимно перпендикулярны, а составляют какой-либо угол между собой, то принципиально рассуждения наши останутся в силе, только геометрические соотношения изменятся. Положение максимумов (пятнышек) будет, конечно, за сеть и от угла между штрихами решеток. Таким образом, по расположению пятнышек можно судить о структуре штриховым поверхности’, о величине периодов и взаимной ориентации решеток.

Если поверхностная структура не периодична, то следует применять для разбора задачи метод Рэлея. Картина  получится более сложной., всевозможно ориентированных решеток (запыленная пластинка, морозные узоры на стекле), то такая структура эквивалентна совокупности простых решеток всех возможных ориентированных, а соответствующая дифракционная картина.

Дифракционные явления на трехмерных структурах

Наибольший интерес и практическое значение имеет дифракцию на пространственных неоднородностях. В этом случае волна распространяется не в однородной среде, а в среде, в которую включая участки, где скорость волны отличается от скорости в остальных частях среды, т. е. участки с иным показателем преломления. Если среда вполне оптически однородна, т. е. показатель преломления любой небольшой  области равняется показателю преломления другой области, то световая волна будет распространяться в среде без изменения направления.

В частности, плоская волна, распространяясь в такой среде останется плоской.  Если же однородность среды нарушена какими-либо включениями или вследствие какого- либо процессов, т. е. если в среде встречаются области, показателя преломления которых отличается от показателя преломления остальной части, то на таких неоднородностях должны возникнуть дифракционные явления, и часть света дифрагирует, отклонив от своего первоначального направления.

Действительно, части волнового фронта, идущие по области различного показателя преломления, распространяются с разной- скоростью, так что фронт волны, т. е. поверхность одинаковой фазы, перестает быть плоским, и свет будет распространяться различным направлениям.

Рассмотрение дифракции на пространственных неоднородностях любой формы представляет собой очень сложную задачу. Мы ограничимся поэтому простейшим случаем, когда неоднородности имеют правильный периодический характер, т. е. представляют собой то, что мы называем решеткой. Однако в этом случае периодическая структура среды имеет пространственный характер, т. е. решетка тянется по всем направлениям в среде. Мы можем представить ее как совокупность периодических структур по трем координатным направлениям и рассматривать дифракцию плоских волн на такой пространственной трехмерной решетке.