Практическое занятие 3

Задача по физике №1

Пучок белого света падает по нормали к поверхности стеклянной пластинки толщиной d=0,4 мкм. Показатель преломления стекла n=1,5. Какие длины волн 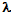, лежащие в пределах видимого спектра ( от 400 до 700 нм), усиливаются в отраженном свете?

Дано:

d = 0,4 мкм =0,4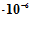м

n=1,5

_________________

-?

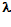Решение задачи:

Условие максимума в отраженном свете:

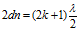Отсюда .

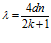При к=1 получаем: .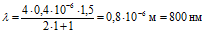

Данная волна не лежит в пределах видимого спектра.

При к=2 получаем: .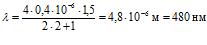

Что удовлетворяет условию.

При к=3 получаем: .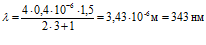

Эта длина также не лежит в пределах видимого спектра. Таким образом, искомая длина волны 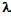=480 нм.

Ответ: длина волны, усиливающая в отраженном свете и лежащая в пределах видимого спектра

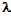=480 нм.

Задача по физике №2

Найти среднее значение длины волны белого света, используя интерференционную картину, полученную от двух узких щелей, расположенных на расстоянии d = 0,02 см одна от другой. Расстояние между темными полосами на экране равно r1 = 0,49 см, а расстояние от щелей до экрана r2 = 200 см.

Дано:

d = 0,02 см

r1 = 0,49 см

r2 = 200 см

__________

-?

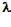Решение задачи:

Расстояние между темными полосами (минимумами света) такие же, как и между светлыми (максимум), поэтому

где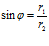

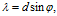
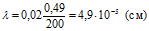
Вычисление:

Ответ: среднее значение длины волны λ=4,9·10־⁵ см.

Задача по физике №3

Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны 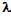=600 нм, падающим по нормали к поверхности пластинки. Найти толщину h воздушного слоя между линзой и стеклянной пластинкой в том месте, где наблюдается четвертое темное кольцо в отраженном свете.

Дано:

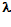=600 нм=0,6ּ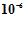м

к=4

_________

h-?

Решение задачи:

Условие минимума в отраженном свете:

2hn=4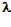

По условию к=4 (число колец), n=1, тогда

2h=4,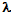

откуда h=2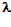

Вычисление:

h = 1,2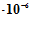(м)

Ответ: толщина воздушного слоя h = 1,2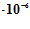 м.

Задача по физике №4

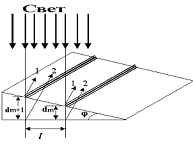
На стеклянный клин падает нормально монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между соседними интерференционными минимумами в отраженном свете равно 2 мм.

Дано:

n=1,5

λ = 698 нм = 6,98۰10^-7 м

l = 2 мм = 2۰10^-3 м

______________________

φ - ?

Решение задачи:

Параллельный пучок света, падая нормально к грани, отражается как от верхней (луч 1), так и от нижней (луч 2) грани клина. Лучи 1 и 2 когерентны между собой и интерферируют. Интерференционная картина представляет собой чередование темных и светлых полос. Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны (условие минимума):

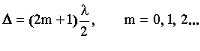
Оптическая разность хода в отраженном свете равна:

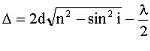
где i - угол падения луча. Так как по условию свет падает нормально, то i = 0 и sini = 0. Произвольной полосе с номером m соответствует толщина d_m , а (m+1) полосе соответствует толщина клина d_m+1 . Запишем условие минимума для двух соседних темных полос:

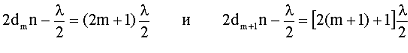
Отсюда: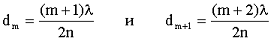   

Тогда: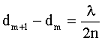   

Из рисунка: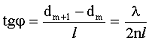   

Вычисление: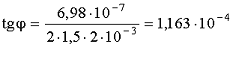

Тангенс мал, поэтому: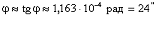   

Ответ: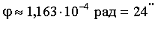

Задача по физике №5

На рисунке 1 изображена схема опыта Френеля по наблюдению интерференции. Два одинаковых плоских зеркала образуют между собой угол π – 2α (2α = 0,1 рад). Точечный источник света S находится на биссектрисе угла на расстоянии d = 20 см от линии пересечения зеркал. При каком минимальном размере зеркал α на удаленном экране могут наблюдаться интерференционные полосы? Прямые лучи от источника на экран не падают.

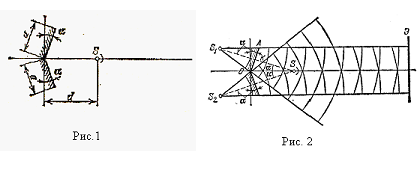
Дано:

d = 20 см = 0,2 м

2α = 0,1 рад; α=0,05 рад

_____________________

α - ?

Решение задачи:

Каждое из зеркал дает мнимое изображение источника S (рис.2). Источники S₁ и S₂ когерентны, так как представляют собой изображение одного и того же источника. Поэтому в той области, где пучки света, исходящие из этих источников, перекрываются, возможно наблюдение интерференционной картины. Ширина пучков определяется положением источника и размерами зеркала. Для того чтобы пучки могли пересечься на удаленном экране, необходимо, чтобы луч, прошедший через край зеркала, шел (при минимальном размере зеркала) параллельно оси системы. При этом

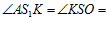α.

Из треугольника АS₁К имеем

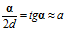(так как угол α мал, то

tg α ≈ α).

Выразим α=2d α

Вычисление:

α=2۰0,2۰0,05=0,02 (м)

Ответ: минимальный размер зеркал α = 2 см.

Задача по физике №6

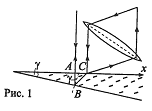Пучок света (λ = 582 нм) падает перпендикулярно к поверхности стеклянного клина. Угол клина γ = 20^″ . Какое число κ_о темных интерференционных полос приходится на единицу длины клина? Показатель преломления стекла n = 1,5.

Дано:

λ = 582 нм = 5,82 ۰ 10^-7 м

γ = 20^″=15,4۰10^-7 рад

n = 1,5

__________

κ_о - ?

Решение:

Для малых углов АВ = ВС = h (рис. 1) и tg = γ. Разность хода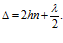

Выразим h через длину участка поверхности клина h=x۰ tg γ ; h= γ x .

Тогда разность хода будет равна 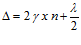- (1)

Если интенсивность интерферирующих волн одинакова, то результирующая интенсивность в точках, для которых разность хода равна 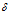, определяется выражением 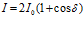- (2),

где 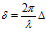- (3)

Подставляя (1) в (3), получим .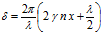

Тогда уравнение (2) примет вид

;

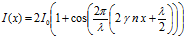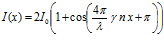- (4)

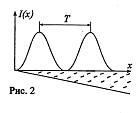
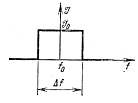
Найдем период колебаний (рис. 2).

Из (4) имеем

; ; .

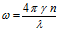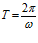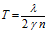Число темных полос, приходящихся на единицу клина, есть величина обратная периоду

.

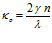Вычисление:

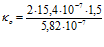= 5 (1/см)

Ответ: число темных полос, приходящихся на единицу клина κ_о = 5 см ^-1.

Задачи для самостоятельного решения

1. Длина волны красного луча в воде равна длине волны зеленого луча в воздухе. Вода освещена красным светом. Какой цвет видит при этом свете человек, открывающий глаза под водой?
2. Какую наименьшую толщину должна иметь прозрачная пластинка, изготовленная из материала с показателем преломления 1,2, чтобы при освещении ее перпендикулярными лучами с длиной волны 600 нм в отраженном свете казалась черной?
3. Лучи света под углом i=45˚ падают на тонкую прозрачную пластинку, которая при этом окрашена в зеленый цвет. Показать, что при уменьшении угла i цвет пластинки должен изменяться, переходя к красному концу спектра, а при увеличении угла i – наоборот, к фиолетовому.
4. При осуществлении интерференции света были получены световые пучки, в состав которых, наряду с когерентным светом, входил и некогерентный. Что при этом наблюдалось?
5. Между двумя стеклянными пластинами l и lˊ образовался воздушный клин с углом 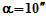. Какой вид будет иметь интерференционная картина при освещении клина перпендикулярно падающим пучком света с длиной волны 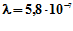м? как изменится интерференционная картина при увеличении угла ?
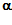6. На расстоянии наилучшего зрения (25см) нормальный человеческий глаз видит раздельно две точки, отстающие одна от другой на 0,07 мм. Определите угол 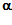между пластинами, при котором глаз перестает различать интерференционные полосы, и наибольшую толщину клина, если его длина l=10 см.
7. Оценить неточность, которую можно допустить в установке углов наклона зеркала в интерферометре Майкельсона для того, чтобы можно было наблюдать полосы равного наклона. Ширина зеркал D = 5 см, длина волны света λ = 0,55 мкм.
8. От двух когерентных источников света S₁ и S₂ получена система интерференционных полос на экране Э, удаленном от источников на расстояние L = 2 м. Во сколько раз изменится ширина интерференционных полос, если между источниками и экраном поместить собирающую линзу с фокусным расстоянием F = 40 см так, чтобы источники S₁ и S₂ оказались в фокальной плоскости линзы?
9. Определить видность ν интерференционной картины от двух точечных источников, спектор излучения которых одинаков. Как зависит видность ν от ширины спектра ∆f ?
10. Установка для получения колец Ньютона освещается белым светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 5 м наблюдение ведется в проходящем свете. Найти радиусы r_с r_кр четвертого синего кольца (λ_с = 400 нм) и третьего красного кольца (λ_кр = 630 нм).