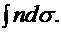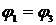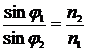Принцип Ферма

Из уравнения эйконала вытекает важное физическое положение, известное как принцип Ферма, согласно которому оптический луч всегда выбирает траекторию с минимальной длиной оптического пути. Только в очень редких случаях условие минимума заменяется условием максимума. Таким образом, лучевые траектории являются экстремалями функционала Ферма

Принцип Ферма

(1)

Принцип Ферма определяет лучевую структуру поля не только в плавно неоднородной среде. Луч, соединяющий две точки r₀ и r₁, выделяется из всех кривых, проходящих через эти точки, тем, что эйконал 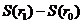(13) экстремален. Из принципа экстремальности может быть выведен закон зеркального отражения

(2)

и закон преломления

(3)

на резкой границе между двумя плавно-неоднородными средами. Здесь n₁ - показатель преломления среды, из которой на границу падает луч. Он преобразуется в два луча - преломленный и отраженный в среду n₂.

Углы φ₁, φ₂, φ₃ - соответственно углы с нормалью падающего, преломленного и отраженного лучей. Все три луча и нормаль к поверхности расположены в плоскости падения. Хотя эти законы получены для случая падения плоской волны на плоскую границу раздела однородных сред, они выполняются и для неплоской границы между плавно неоднородными средами, если поле сохраняет лучевую структуру (9).