Дифракция Френеля на краю полуплоскости и на щели
Дифракция от прямолинейного края полуплоскости
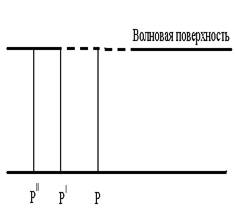
Поместим на пути световой волны непрозрачную полуплоскость с прямолинейным краем. Расположим эту полуплоскость так, чтобы она совпала с одной из волновых поверхностей. На расстоянии b за полуплоскостью поставим параллельный ей экран, на котором возьмем точку Р. Разобьем открытую часть волновой поверхности на зоны, имеющие вид очень узких прямолинейных полосок, параллельных краю полуплоскости. Ширину зон выберем так, чтобы отсчитанные в плоскости рисунка расстояния от точки Р до краев любой зоны отличались на одинаковую величину ∆. При этом условии колебания, создаваемые в точке Р соединим зонами, будут отличаться по фазе на постоянную величину.
Зонами, расположенным справа от точки Р, припишем номера 1, 2, 3, и т.д., расположенные слева- номерами 1' 2' 3'.Зоны с номерами m и m' имеют одинаковую ширину и расположены относительно точки Р симметрично. Поэтому создаваемые ими в Р колебания совпадают по амплитуде и по фазе.
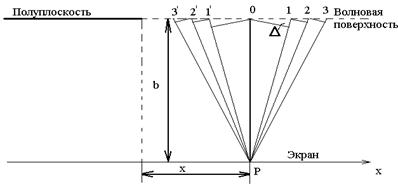
Рис. 5.6.1. Дифракция от прямолинейного края полуплоскости
Дифракция от щели
Бесконечно длинную щель можно образовать, расположив рядом две обращенные в разные стороны полуплоскости. Следовательно, задача о дифракции Френеля от щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу (рис 5.6.2.)
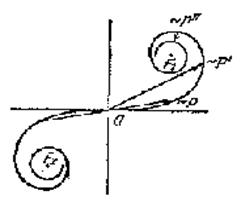
Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали (рис 5.6.3.) Если стремиться в точку Р', лежащую против края щели, начало результирующего вектора переместиться в середину спирали О.
Конец вектора переместиться по спирали в направлении полюса F1. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга. Интенсивность света достигает при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки Р в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.
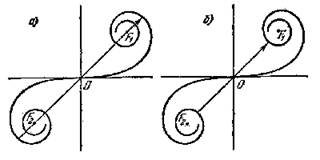
Если изменить ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (рис.5.6.4,а) и отличные от нуля минимумы (рис.5.6.4,б)
Итак, френелевская дифракционная картина от щели представляет собой либо светлую (рис.5.6.4,а), либо относительно темную (рис.5.6.4,б) центральную полосу, по обе стороны которой располагаются симметричные относительно нее чередующиеся темные и светлые полосы.
При большей ширине щели начало и конец результирующего вектора для точки Р лежат на внутренних витках спирали вблизи полос F1 и F2. Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и темных полос.
