Принцип суперпозиции и интенсивность волн

Рассмотрим возмущение, возникающее при одновременном действии двух или нескольких осцилляторов. Простейшая гипотеза , которую можно принять в отношении их совместного действия , заключается в следующем: если 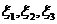 и т.д. - возмущения, производимые  каждым  отдельным осциллятором в какой-либо точке пространства в данный момент времени , а  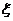- результирующее возмущение, то

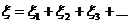(2.4.1)

Принцип суперпозиции

Если результирующее движение описывается волновым уравнением , то необходимо , чтобы 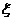 тоже было решением этого уравнения решения волнового уравнения аддитивны , и следовательно ,(2.4.1) есть решение волнового уравнения . Здесь следует подчеркнуть , что этот математический результат сам по  себе не гарантирует , что (2.4.1) точно описывает эффект одновременного действия нескольких волн в данной точке. Принцип суперпозиции есть физическая гипотеза, согласно которой для световых волн возмущение, создающееся при прохождении ряда волн, равно алгебраической сумме возмущений , производимых каждой волной в отдельности. Уравнение (2.4.1) является математической формулировкой этого принципа . Высказанная гипотеза справедлива в той мере , в какой основанные на ней вычисления удовлетворительно описывают соответствующие оптические эксперименты.

При исследовании звуковых волн было найдено , что для волн большой амплитуды скорость распространения зависит от их амплитуды .Было так же установлено , что при одновременной работе двух громких источников звука разной частоты слышны их суммовой и разностный тона. Для описания таких явлений необходимо предположить , что простая форма волн не точно передает свойства звуковых волн конечной амплитуды и что возмущение 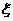, возникающее при одновременном действии двух источников звука, дается соотношением

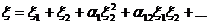(2.4.2)

где 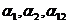- константы, малые по сравнению с .

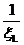Интенсивность волн

Подобные гипотезы потребовалось бы ввести , если бы соответствующие явления наблюдались и при исследовании света; однако до сих пор все попытки обнаружить такие эффекты давали отрицательные результаты. Шредингер рассмотрел результаты , получающиеся при введении некоторых нелинейных членов (вида, предложенного Борном) в уравнении распространении электромагнитных волн. Расчеты показали , что при очень больших интенсивностях скорость света должна зависеть от

Амплитуды, но в практически осуществимых условиях эффект слишком мал, чтобы его можно было наблюдать на опыте.