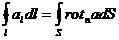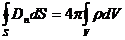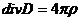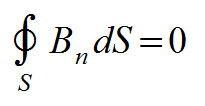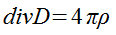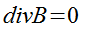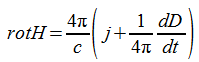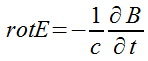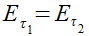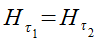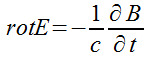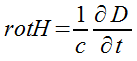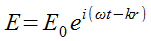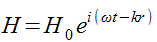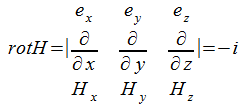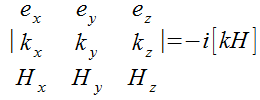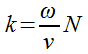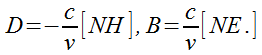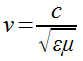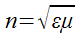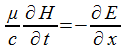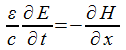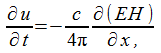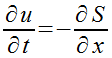Свойства электромагнитных волн

Система уравнений Максвелла

Приведем законы, которым подчиняется поведение электрического и магнитного полей, лежащие в основе теории электромагнетизма. Эти законы, являющиеся обобщением опыта, формулируются ниже в интегральной форме, так как именно в таком виде обычно выражаются данные эксперимента. Используя основные положения векторного анализа, можно записать эти законы электромагнитного поля в дифференциальной форме.

Если исследуют электромагнитное поле в каком-либо веществе, изотропно заполняющем пространство, то значение векторов Е и В получаются при усреднении микроскопических величин <Eмикр>=Е и <Hмикр>=В. Такая запись позволяет оперировать с мгновенными напряженностями электрического и магнитного полей в любой точке пространства.

Усреднение микроскопических величин законно в том случае, линейные размеры области, где <Eмикр> и <Hмикр> можно считать неизменными ,значительно превышают размеры атомов (молеукл). Длина волны 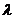 является тем отрезком , на котором напряженность поля сильно изменяется. Поэтому усреднение можно проводить лишь в том случае, когда 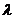значительно больше атомных размеров .Такое равенство соблюдается для всего оптического диапазона спектра, включая короткие ультрафиолетовые лучи. Сложнее обстоит дело в рентгеновской области спектра, где  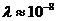см, т.е. того же порядка что размеры атомов.

При переходе к дифференциальной форме законов электромагнитного поля используют следующие теоремы векторного анализа:

Теорема Гаусса о преобразовании поверхностного интеграла в объемный: 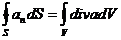 .        (2.3.1)

Теорема Стокса о преобразовании интеграла по замкнутой кривой в поверхностный интеграл (поток ротора через поверхность, охватываемую исследуемой кривой):

.         (2.3.2)

Итак , вспомним законы электрического и магнитного полей. Первый из них - основной закон электростатики - закон Кулона. Как следствие этого закона формулируется теорема Гаусса о потоке, которая при наличии диэлектриков в исследуемом пространстве записывается в виде

.        (2.3.3)

Отсюда указанным выше способом переходим к дифференциальной форме закона

,             (2.3.3а)

где D - вектор электрического смещения, 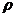- объемная плотность зарядов.

Существенно, что выражения (2.3.3) и (2.3.3а), полученные из уравнений электростатики, обобщаются Максвеллом для переменных полей, где D и 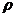 зависят от времени .

Отсутствие в природе магнитных зарядов (монополей) приводит к выражению

(2.3.4)

которое преобразуется к виду

div B = 0. (2.3.4а)

Эти формулы соответствуют хорошо известным модельным представлением о силовых линиях электрического поля, начинающихся на положительных зарядах и  заканчивающихся на отрицательных, тогда как линии магнитного поля замкнуты и охватывают породившие их токи. Введение понятия линий электрического и магнитного полей совершенно не обязательно (смысл законов содержится в приведенных формулах), но, как и во многих случаях, наглядность модельных  представлений помогает пониманию явления.

Переходя к описанию свойств электрического тока. сформулируем основной закон о зависимости напряженности магнитного поля от силы породившего его тока. Этот закон обычно связывают с именами Био, Савара и Лаплпса. Запишем его в виде, который называют теоремой о циркуляции вектора Н:

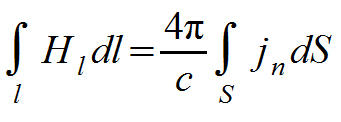
Рис. 2.3.5. Теорема о циркуляции вектора Н

Дифференциальная форма этого закона получается применением теоремы Стокса к равенству (2.3.5) и описывает плотности тока  j с напряженностью магнитного поля в данной точке:

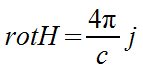
Рис. 2.3.6. Теорема Стокса

Как известно, Максвелл ввел ток смещения, плотность которого удовлетворяет соотношению

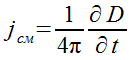
плотность тока

Ток проводимости и ток смещения дополняют друг друга, образуя полный ток плотностью

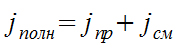
плотность полного тока

которая, согласно Максвеллу, и фигурирует в уравнении (2.3.6) последним из требующихся нам фундаментальных соотношений является математическая формулировка знаменитого открытия Фарадея - закона электромагнитной индукции.

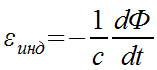
Рис. 2.3.7. Закон электромагнитной индукции

в котором электродвижущая сила 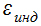, возникающая в замкнутом контуре, связывается со скоростью изменения потока магнитной индукции Ф, пронизывающего этот контур.

При соблюдении некоторых условий эксперимента ( в частности , если контур с током неподвижен и не деформируется за время изменений ) справедлива следующая интегральная форма записи закона индукции:

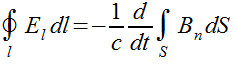
Рис. 2.3.8. Интегральная форма записи закона индукции

откуда легко получается дифференциальная форма закона

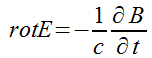
Рис. 2.3.9. Дифференциальная форма записи закона индукции

Здесь уместно сделать следующее значения:

1. Хорошо известны соображения о вихревом характере электрического поля, порождаемого изменяющимся во времени магнитным полем. Это переменное электрическое поле существенно отличается от потенциального электростатического поля , создаваемого системой неподвижных электрических зарядов, для которого rotE = 0. В последующем нас будет интересовать именно переменное электрическое поле . Но , как было показано Максвеллом , наличие переменного электрического поля с неизбежностью приводит к возникновению связанного с ним магнитного поля и поэтому нужно говорить о едином электромагнитном поле , характеризуемом в каждой точке пространства взаимосвязанными ортогональными векторами Е и В.

2. Введение Максвеллом понятий тока смещения в начале выглядело как гениальная догадка. Но несовместимость сформулированного уравнения электромагнитного поля (2.3.6) и уравнения непрерывности

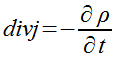
Рис. 2.3.10. Уравнение непрерывности

выражающего одно из самых общих свойств материи - закон сохранения электрического заряда, - с неизбежностью приводит к необходимости введения дополнительного слагаемого  в правую часть уравнения поля. Следовательно, уравнение (2.3.6) должно иметь вид

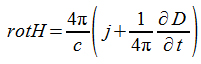
Уравнение теоремы Стокса

Именно это изменяющееся во времени электрическое поле , столь неудачно названо «током смещения», и связанное с ним магнитное поле будут играть главную роль в дальнейшем  изложении.

Итак, имеем уравнение электромагнитного поля в следующем виде:

,  ,

, .      (2.3.11)

Их нужно дополнить «материальными» уравнениями, учитывающими соотношения между векторами Е,D,В,Н и j. При отсутствии ферромагнитных сегнетоэлектрических материалов для изотропных сред можно записать эти уравнения при помощи трех констант: 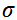 (электропроводность),  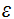(диэлектрическая проницаемость) и  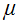(магнитная проницаемость), постулируя линейную связь между D и Е, В и Н, j и E, т.е.

D =E , В = Н, j = E.                     (2.3.12)

Следует также сформулировать граничные условия для уравнений электромагнитного поля, из которых наиболее широко будем использовать равенство тангенциальных составляющих Е и Н на границе раздела двух сред, т.е.

,  (2.3.13)

если предположить, что граничащие среды разделены слоем, в котором константы 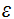, 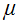и 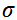изменяются непрерывно, а j и 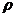конечны, то при стремлении к нулю толщины этого слоя уравнения (2.3.9) и (2.3.6) сведутся к равенствам (2.3.14). Однако при решении конкретных задач часто возникает необходимость задать значение искомых функций на границе исследуемой области. Такие граничные условия определяются условиями эксперимента и не вытекают из уравнений электромагнитного поля. Они должны быть добавлены к системе уравнений (2.3.11). В частности, при рассмотрении безграничного пространства часто задают вид тех или иных функций на бесконечности, руководствуясь физическими условиями решаемой задачи.

Система уравнений, включающая в себя уравнения электромагнитного поля, «материальные» соотношения и граничные условия, названа системой уравнений Максвелла и играет в электродинамике ту же роль. что и аксиоматика уравнений Ньютона в классической механике.

Поперечность электромагнитных волн

Допустим, что волны распространяются в однородном незаряженном диэлектрике. Применим к ним фундаментальные уравнения Максвелла

И материальные уравнения D =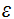E , В = 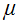Н.

Пусть волна - плоская и монохроматическая. Запишем ее в комплексном виде

,  (2.3.15)

где 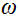 - круговая частота, k- волновой вектор, а амплитуды  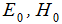постоянны. Дифференцируя по времени, получаем 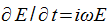, т.е. операция дифференцирования в этом случае сводится к умножению на 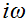. Аналогично, дифференцирование по координатам x, y, z сводится к умножению на 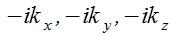. Заметив это и обозначая координатные орты через  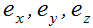получаем

и аналогично для rot E. В результате уравнения Максвелла перейдут в

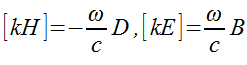
Рис. 2.3.16. Уравнение Максвелла

Введем единичный вектор N нормали к фронту волны и скорость распространения последнего в направлении этой нормали - так называемую нормальную скорость v.

Тогда  (2.3.17)

И предыдущие соотношения перейдут в

 (2.3.18)

отсюда видно, что векторы E, H, v в плоской электромагнитной волне взаимно перпендикулярны . Перпендикулярность векторов Е и Н к вектору v, или, что то же, к направлению распространения волны, означает, что электромагнитные волны поперечны. Т.е. проблема поперечности световых волн, с которой не могли справиться теории механического эфира, совсем не возникает в электромагнитной теории света.

Скорость электромагнитной волны

Из уравнений Максвелла можно определить и скорость электромагнитной волны v. С этой целью запишем эти уравнения в скалярной форме:

или

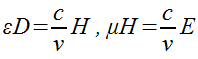Отсюда после почленного перемножения и сокращения на ЕН получаем для v и показателя преломления  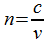следующие выражения:

,

Последнее соотношение  называется законом Максвелла. Для немагнитных сред (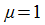) оно переходит в .

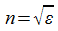В вакууме v=c, т.е. v совпадает с электродинамической постоянной с. Тем самым раскрывается глубокий смысл открытия В.Вебера и Кольрауша, впервые измеривших эту постоянную в 1856г.

Энергия переносимая электромагнитной волной

Электромагнитная волна представляет собой электромагнитное возмущение распространяющееся, как уже говорилось, в вакууме со скорость c, а в среде - со скоростью 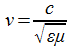. С этим электромагнитным возмущением связанна энергия, плотность которой (т.е. энергия, заключенная в единице объема) выражается для электрического поля через 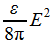, а для магнитного поля через 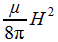. В случае монохроматической волны  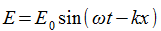и , так что энергия волны пропорциональна квадрату ее амплитуды. Это соотношение между энергией и амплитудой сохраняет свое значение и для любой другой волны.

При распространении электромагнитной волны происходит перенос энергии, подобно тому как это имеет место при распространении упругой волны. Вопрос о течении энергии в упругой волне был впервые (1874г.) рассмотрен Н. А. Умовым который доказал общую теорему о потоке энергии в любой среде. Поток энергии в упругой волне может быть вычислен через величины, характеризующие потенциальную энергию упругой деформации и кинетическую энергию движения частиц упругой среды. Плотность потока энергии выражается с помощью специального вектора (вектор Умова). Аналогичное рассмотрение плодотворно и для электромагнитных. До известной степени можно уподобить энергию электрического поля потенциальной энергии упругой деформации, а энергию магнитного поля - кинетической энергии движения частей деформированного тела. Так же как и в случае упругой деформации, передача энергии от точки к точке в электромагнитной волне связанна с тем обстоятельством, что волны электрической магнитной напряженности находятся в одной фазе. Такая волна называется бегущей. Движение энергии в бегущей упругой волне удобно изображается с помощью вектора S, который можно назвать вектором энергии и который показывает, какое количество энергии протекает в волне за 1с. через 1 метр в квадрате. Для электромагнитных волн вектор этот был введен Пойтингом (1884г.) Его уместно называть вектором Умова-Пойтинга.

Нетрудно найти выражение этого вектора для простого случая, рассмотренного нами в пункте 2.2 и выражающего распространение полоской электромагнитной волны вдоль оси x.

Умножив  на Н и  на Е и сложив,

получим

где 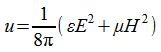 есть плотность энергии. Рассматривая поток энергии S, входящий и выходящий из элементарного объема, найдем выражение для изменения плотности энергии по времени

Отсюда

Рис. 2.3.19. Численное выражение вектора Умова – Пойтинга для электромагнитной волны

что представляет собой численное выражение вектора Умова - Пойтинга для электромагнитной волны. Что касается направления вектора Умова - Пойтинга, то он перпендикулярен к плоскости, проходящей через векторы электрической м магнитной напряженности, т.е. в векторной форме запишется в общем виде

Своим направление вектор Умова - Пойтинаг определяет направление переноса энергии волны и может бать во многих случаях принят за направление светового луча. Не следует, однако, забывать, что понятие луча есть понятие геометрической оптики и не имеет вполне соответствующего образа в области волновых представлений, для которых введен вектор Умова - -Пойтинга.